


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-4-2021
Date: 22-2-2021
Date: 10-3-2021
|
The mathematical study of the likelihood and probability of events occurring based on known information and inferred by taking a limited number of samples. Statistics plays an extremely important role in many aspects of economics and science, allowing educated guesses to be made with a minimum of expensive or difficult-to-obtain data.
A joke told about statistics (or, more precisely, about statisticians), runs as follows. Two statisticians are out hunting when one of them sees a duck. The first takes aim and shoots, but the bullet goes sailing past six inches too high. The second statistician also takes aim and shoots, but this time the bullet goes sailing past six inches too low. The two statisticians then give one another high fives and exclaim, "Got him!" (This joke plays on the fact that the mean of 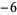 and 6 is 0, so "on average," the two shots hit the duck.)
and 6 is 0, so "on average," the two shots hit the duck.)
Approximately 73.8474% of extant statistical jokes are maintained by Ramseyer.
REFERENCES:
Babu, G. and Feigelson, E. Astrostatistics. New York: Chapman & Hall, 1996.
Bernstein, S. and Bernstein, R. Theory and Problems of Elements of Statistics I: Descriptive Statistics and Probability. New York: McGraw-Hill, 1999.
Dixon, W. J. and Massey, F. J. Introduction to Statistical Analysis, 4th ed. New York: McGraw-Hill, 1983.
Everitt, B. Chance Rules: An Informal Guide to Probability, Risk, and Statistics. Copernicus, 1999.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, 1968.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 2, 2nd ed. New York: Wiley, 1968.
Fisher, N. I.; Lewis, T.; and Embleton, B. J. J. Statistical Analysis of Spherical Data. Cambridge, England: Cambridge University Press, 1987.
Fisher, R. A. and Prance, G. T. The Design of Experiments, 9th ed. rev. New York: Hafner, 1974.
Fisher, R. A. Statistical Methods for Research Workers, 14th ed., rev. and enl. Darien, CO: Hafner, 1970.
Gonick, L. and Smith, W. The Cartoon Guide to Statistics. New York: Harper Perennial, 1993.
Goulden, C. H. Methods of Statistical Analysis, 2nd ed. New York: Wiley, 1956.
Hoel, P. G.; Port, S. C.; and Stone, C. J. Introduction to Statistical Theory. New York: Houghton Mifflin, 1971.
Hogg, R. V. and Tanis, E. A. Probability and Statistical Inference, 5th ed. Englewood Cliffs, NJ: Prentice-Hall, 1996.
Keeping, E. S. Introduction to Statistical Inference. New York: Dover, 1995.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, 1962.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.
MathPages. "Probability." https://www.mathpages.com/home/iprobabi.htm.
Mises, R. von Mathematical Theory of Probability and Statistics. New York: Academic Press, 1964.
Mises, R. von Probability, Statistics, and Truth, 2nd rev. English ed. New York: Dover, 1981.
Mood, A. M. Introduction to the Theory of Statistics. New York: McGraw-Hill, 1950.
Neyman, J. First Course in Probability and Statistics. New York: Holt, 1950.
O'Hagan, A. Kendall's Advanced Theory of Statistics, Vol. 2B: Bayesian Inference, 6th ed. New York: Oxford University Press, 1998.
Ostle, B. Statistics in Research: Basic Concepts and Techniques for Research Workers, 4th ed. Ames, IA: Iowa State University Press, 1988.
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, 1984.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Statistical Description of Data." Ch. 14 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 603-649, 1992.
Pugh, E. M. and Winslow, G. H. The Analysis of Physical Measurements. Reading, MA: Addison-Wesley, 1966.
Ramseyer, G. "First Internet Gallery of Statistics Jokes." https://www.ilstu.edu/~gcramsey/Gallery.html.
Robbins, H. and van Ryzin, J. Introduction to Statistics. Chicago, IL: Science Research Associates, 1975.
Snedecor, G. W. Statistical Methods Applied to Experiments in Agriculture and Biology, 5th ed. Ames, IA: State College Press, 1956.
Spiegel, M. R. and Stephens, L. J. Theory and Problems of Statistics, 3rd ed. New York: McGraw-Hill, 1998.
Stuart, A.; and Ord, J. K. Kendall's Advanced Theory of Statistics, Vol. 1: Distribution Theory, 6th ed. New York: Oxford University Press, 1998.
Stuart, A.; and Ord, J. K. Kendall's Advanced Theory of Statistics, Vol. 2A: Classical Inference & the Linear Model, 6th ed. New York: Oxford University Press, 1999.
Székely, G. J. Paradoxes in Probability Theory and Mathematical Statistics, rev. ed. Dordrecht, Netherlands: Reidel, 1986.
Tippett, L. H. C. The Methods of Statistics: An Introduction Mainly for Experimentalists, 3rd rev. ed. London: Williams and Norgate, 1941.
Tukey, J. W. Exploratory Data Analysis. Reading, MA: Addison-Wesley, 1977.
Uspensky, J. V. Introduction to Mathematical Probability. New York: McGraw-Hill, 1937.
Weisstein, E. W. "Books about Statistics." https://www.ericweisstein.com/encyclopedias/books/Statistics.html.
Whittaker, E. T. and Robinson, G. The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, 1967.
Young, H. D. Statistical Treatment of Experimental Data. New York: McGraw-Hill, 1962.
Yule, G. U. and Kendall, M. G. An Introduction to the Theory of Statistics, 14th ed., rev. and enl. New York: Hafner, 1950.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|