
Delta Function in a Box
 المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 2 , p 54
الجزء والصفحة:
part 2 , p 54
 14-8-2016
14-8-2016
 1682
1682
Delta Function in a Box
A particle of mass m is confined to a box, in one dimension, between –a < x < a, and the box has walls of infinite potential. An attractive delta function V(x) = -aCδ(x) is at the center of the box.
a) What are the eigenvalues of odd-parity states?
b) Find the value of C for which the lowest eigenvalue is zero.
c) Find the ground state wave function for the case that the lowest eigenvalue is less than zero energy.
SOLUTION
a) In the absence of the delta function potential, the states with odd parity are
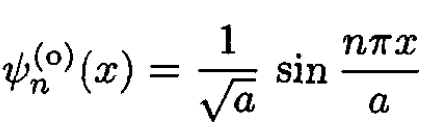 (1)
(1)
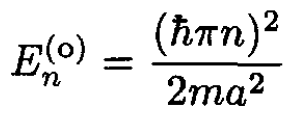 (2)
(2)
These states have zero amplitude at the site of the delta function x = 0 and are unaffected by it. So, the states with odd parity have the same eigenfunction and eigenvalues as when the delta function is absent.
b), c) For a delta function potential without a box, the bound states have a wave function of Ae-α|x|. In the box we expect to have similar exponentials, except that the wave function must vanish at the edges of the box (x = ±a). The states which do this are
 (3)
(3)
 (4)
(4)
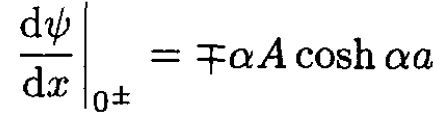 (5)
(5)
Using (S.5.4.1), we match the difference in the derivatives at x = 0 with the amplitude of the delta function potential. This leads to the eigenvalue condition
 (6)
(6)
 (7)
(7)
The quantity on the left of (6) has a minimum value of 1, which it obtains at α → 0. This limit produces the eigenvalue E = 0. So we must have C = C0 for the zero eigenvalue, which is the answer to part (b). The above eigenfunction, for values of α > 0, gives the bound state energy E < 0 when C > C0.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


