


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-3-2021
Date: 30-3-2021
Date: 11-2-2021
|
If 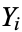 have normal independent distributions with mean 0 and variance 1, then
have normal independent distributions with mean 0 and variance 1, then
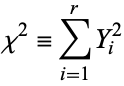 |
(1) |
is distributed as 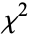 with
with 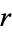 degrees of freedom. This makes a
degrees of freedom. This makes a 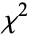 distribution a gamma distribution with
distribution a gamma distribution with 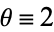 and
and 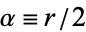 , where
, where 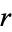 is the number of degrees of freedom.
is the number of degrees of freedom.
More generally, if 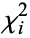 are independently distributed according to a
are independently distributed according to a 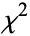 distribution with
distribution with 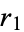 ,
, 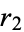 , ...,
, ..., 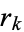 degrees of freedom, then
degrees of freedom, then
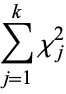 |
(2) |
is distributed according to 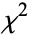 with
with 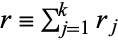 degrees of freedom.
degrees of freedom.
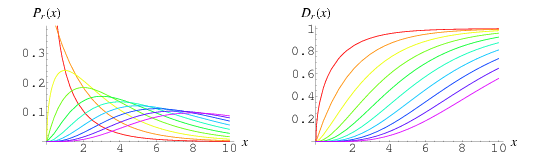
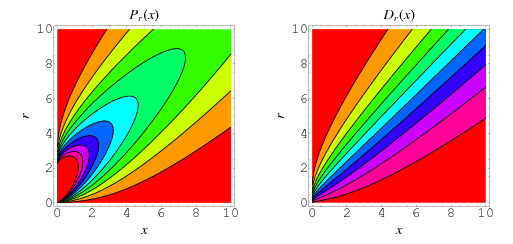
The probability density function for the 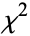 distribution with
distribution with 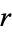 degrees of freedom is given by
degrees of freedom is given by
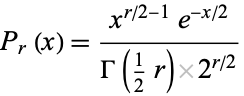 |
(3) |
for 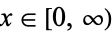 , where
, where 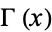 is a gamma function. The cumulative distribution function is then
is a gamma function. The cumulative distribution function is then
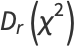 |
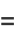 |
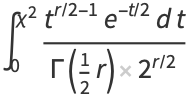 |
(4) |
 |
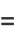 |
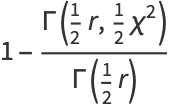 |
(5) |
 |
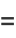 |
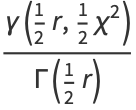 |
(6) |
 |
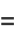 |
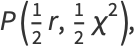 |
(7) |
where 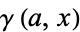 is an incomplete gamma function and
is an incomplete gamma function and 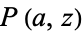 is a regularized gamma function.
is a regularized gamma function.
The chi-squared distribution is implemented in the Wolfram Language as ChiSquareDistribution[n].
For 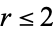 ,
, 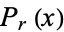 is monotonic decreasing, but for
is monotonic decreasing, but for 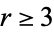 , it has a maximum at
, it has a maximum at
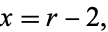 |
(8) |
where
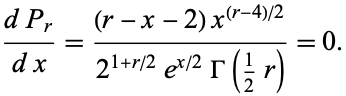 |
(9) |
The 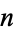 th raw moment for a distribution with
th raw moment for a distribution with 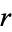 degrees of freedom is
degrees of freedom is
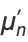 |
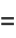 |
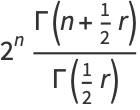 |
(10) |
 |
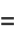 |
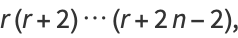 |
(11) |
giving the first few as
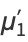 |
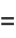 |
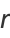 |
(12) |
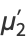 |
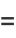 |
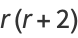 |
(13) |
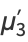 |
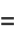 |
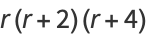 |
(14) |
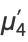 |
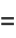 |
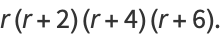 |
(15) |
The 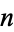 th central moment is given by
th central moment is given by
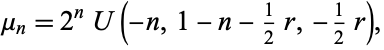 |
(16) |
where 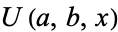 is a confluent hypergeometric function of the second kind, giving the first few as
is a confluent hypergeometric function of the second kind, giving the first few as
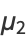 |
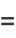 |
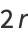 |
(17) |
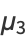 |
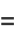 |
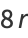 |
(18) |
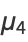 |
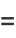 |
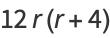 |
(19) |
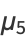 |
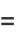 |
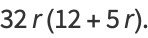 |
(20) |
The cumulants can be found via the characteristic function
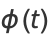 |
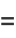 |
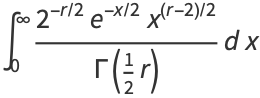 |
(21) |
 |
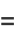 |
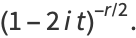 |
(22) |
Taking the natural logarithm of both sides gives
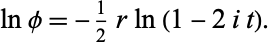 |
(23) |
But this is simply a Mercator series
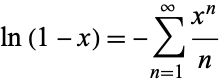 |
(24) |
with 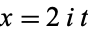 , so from the definition of cumulants, it follows that
, so from the definition of cumulants, it follows that
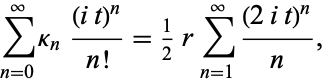 |
(25) |
giving the result
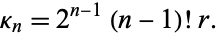 |
(26) |
The first few are therefore
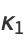 |
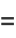 |
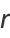 |
(27) |
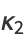 |
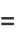 |
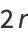 |
(28) |
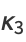 |
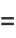 |
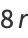 |
(29) |
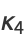 |
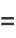 |
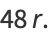 |
(30) |
The moment-generating function of the 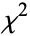 distribution is
distribution is
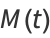 |
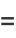 |
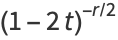 |
(31) |
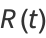 |
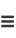 |
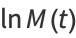 |
(32) |
 |
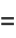 |
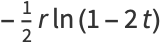 |
(33) |
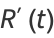 |
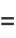 |
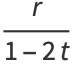 |
(34) |
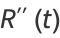 |
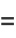 |
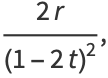 |
(35) |
so
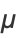 |
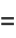 |
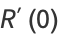 |
(36) |
 |
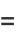 |
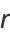 |
(37) |
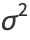 |
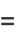 |
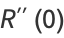 |
(38) |
 |
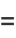 |
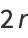 |
(39) |
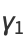 |
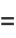 |
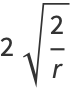 |
(40) |
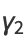 |
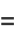 |
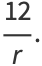 |
(41) |
If the mean is not equal to zero, a more general distribution known as the noncentral chi-squared distribution results. In particular, if 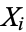 are independent variates with a normal distribution having means
are independent variates with a normal distribution having means 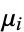 and variances
and variances 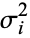 for
for 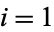 , ...,
, ..., 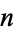 , then
, then
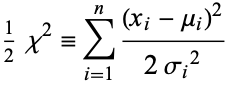 |
(42) |
obeys a gamma distribution with 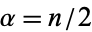 , i.e.,
, i.e.,
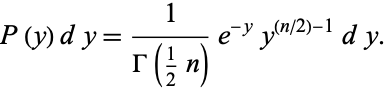 |
(43) |
where 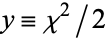 .
.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 940-943, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 535, 1987.
Kenney, J. F. and Keeping, E. S. "The Chi-Square Distribution." §5.3 in Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, pp. 98-100, 1951.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Incomplete Gamma Function, Error Function, Chi-Square Probability Function, Cumulative Poisson Function." §6.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 209-214, 1992.
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, pp. 115-116, 1992.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|