
Commutative Diagram
 المؤلف:
Cartan H. and Eilenberg, S
المؤلف:
Cartan H. and Eilenberg, S
 المصدر:
Homological Algebra. Princeton, NJ: Princeton University Press, 1956.
المصدر:
Homological Algebra. Princeton, NJ: Princeton University Press, 1956.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 8-5-2021
8-5-2021
 2235
2235
Commutative Diagram
A commutative diagram is a collection of maps 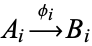 in which all map compositions starting from the same set
in which all map compositions starting from the same set  and ending with the same set
and ending with the same set  give the same result. In symbols this means that, whenever one can form two sequences
give the same result. In symbols this means that, whenever one can form two sequences
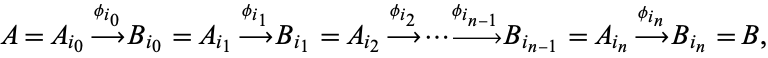 |
(1)
|
and
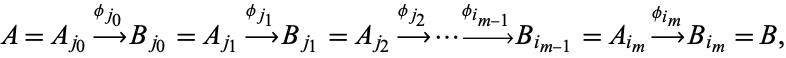 |
(2)
|
the following equality holds:
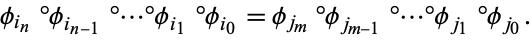 |
(3)
|
Commutative diagrams are usually composed by commutative triangles and commutative squares.
Commutative triangles and squares can also be combined to form plane figures or space arrangements.

A commutative diagram can also contain multiple arrows that indicate different maps between the same two sets.
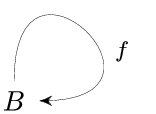
A looped arrow indicates a map from a set to itself.
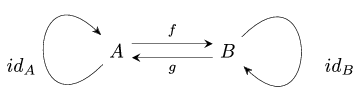
The above commutative diagram expresses the fact that 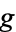 is the inverse map to
is the inverse map to 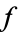 , since it is a pictorial translation of the map equalities
, since it is a pictorial translation of the map equalities 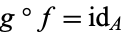 and
and 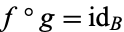 .
.
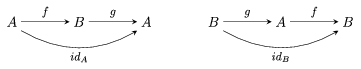
This can also be represented using two separate diagrams.
Many other mathematical concepts and properties, especially in algebraic topology, homological algebra, and category theory, can be formulated in terms of commutative diagrams.
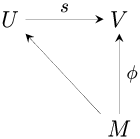
For example, a module  is projective iff any surjective module homomorphism
is projective iff any surjective module homomorphism 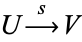 and any module homomorphism
and any module homomorphism 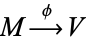 can be completed to a commutative diagram.
can be completed to a commutative diagram.
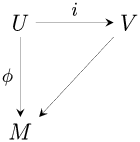
Similarly, one can characterize the dual notion of injective module: a module  is injective iff any injective module homomorphism and
is injective iff any injective module homomorphism and 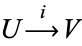 and any module homomorphism
and any module homomorphism 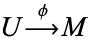 can be completed to a commutative triangle.
can be completed to a commutative triangle.
According to Baer's criterion, it is sufficient to require this condition for the inclusion maps 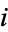 of the ideals of
of the ideals of 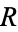 in
in 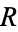 .
.
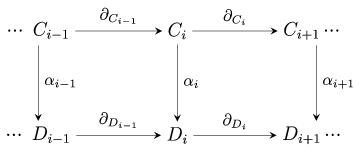
Another example of a notion based on diagrams is the chain homomorphism, which can be visualized as a sequence of commutative squares.
The advantage of drawing commutative diagrams is the possibility to seize any given map configuration at a glance. The picture also facilitates the task of composing maps, which is like following directed paths from set to set. Many homological theorems are proven by studying commutative diagrams: this method is usually referred to as "diagram chasing."
REFERENCES:
Bourbaki, N. "Diagrammes commutatifs." §1.1 in Algèbre. Chap. 10, Algèbre Homologique. Paris, France: Masson, 1-3, 1980.
Cartan H. and Eilenberg, S. Homological Algebra. Princeton, NJ: Princeton University Press, 1956.
Davis, J. F. and Kirk, P. Lecture Notes in Algebraic Topology. Providence, RI: Amer. Math. Soc., 2001.
Eilenberg, S. and Steenrod, N. Foundations of Algebraic Topology. Princeton, NJ: Princeton University Press, 1952.
Herrlich, H. and Strecker, G. E. Category Theory: An Introduction. Boston, MA: Allyn and Bacon, 1973.
Hilton, P. J. and Stammbach, U. A Course in Homological Algebra, 2nd ed. New York: Springer-Verlag, 1997.
Lang, S. Algebra, rev. 3rd ed. New York: Springer-Verlag, 2002.
Mac Lane, S. Categories for the Working Mathematician. New York: Springer-Verlag, 1971.
Mac Lane, S. Homology. Berlin: Springer-Verlag, 1967.
Mitchell, B. Theory of Categories. New York: Academic Press, 1965.
Northcott, D. G. An Introduction to Homological Algebra. Cambridge, England: Cambridge University Press, 1966.
Rotman, J. J. An Introduction to Algebraic Topology. New York: Springer-Verlag, 1988.
Scott Osborne, M. Basic Homological Algebra. New York: Springer-Verlag, 2000.
 الاكثر قراءة في التبلوجيا
الاكثر قراءة في التبلوجيا
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


