


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-8-2021
Date: 3-6-2021
Date: 10-7-2021
|
Given a map 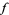 from a space
from a space 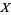 to a space
to a space 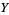 and another map
and another map 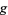 from a space
from a space 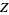 to a space
to a space 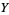 , a lift is a map
, a lift is a map 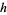 from
from 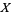 to
to 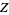 such that
such that 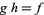 . In other words, a lift of
. In other words, a lift of 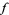 is a map
is a map 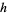 such that the diagram (shown below) commutes.
such that the diagram (shown below) commutes.
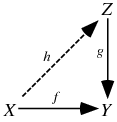
If 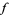 is the identity from
is the identity from 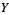 to
to 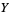 , a manifold, and if
, a manifold, and if 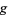 is the bundle projection from the tangent bundle to
is the bundle projection from the tangent bundle to 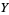 , the lifts are precisely vector fields. If
, the lifts are precisely vector fields. If 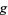 is a bundle projection from any fiber bundle to
is a bundle projection from any fiber bundle to 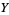 , then lifts are precisely sections. If
, then lifts are precisely sections. If 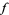 is the identity from
is the identity from 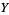 to
to 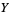 , a manifold, and
, a manifold, and 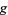 a projection from the orientation double cover of
a projection from the orientation double cover of 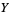 , then lifts exist iff
, then lifts exist iff 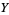 is an orientable manifold.
is an orientable manifold.
If 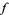 is a map from a circle to
is a map from a circle to 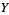 , an
, an 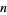 -manifold, and
-manifold, and 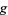 the bundle projection from the fiber bundle of alternating n-forms on
the bundle projection from the fiber bundle of alternating n-forms on 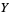 , then lifts always exist iff
, then lifts always exist iff 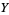 is orientable. If
is orientable. If 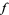 is a map from a region in the complex plane to the complex plane (complex analytic), and if
is a map from a region in the complex plane to the complex plane (complex analytic), and if 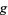 is the exponential map, lifts of
is the exponential map, lifts of 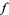 are precisely logarithms of
are precisely logarithms of 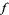 .
.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|