The Alexander polynomial is a knot invariant discovered in 1923 by J. W. Alexander (Alexander 1928). The Alexander polynomial remained the only known knot polynomial until the Jones polynomial was discovered in 1984. Unlike the Alexander polynomial, the more powerful Jones polynomial does, in most cases, distinguish handedness.

In technical language, the Alexander polynomial arises from the homology of the infinitely cyclic cover of a knot complement. Any generator of a principal Alexander ideal is called an Alexander polynomial (Rolfsen 1976). Because the Alexander invariant of a tame knot in 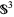 has a square presentation matrix, its Alexander ideal is principal and it has an Alexander polynomial denoted .

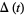Let 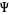 be the matrix product of braid words of a knot, then

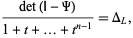(1)

where 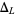 is the Alexander polynomial and det is the determinant. The Alexander polynomial of a tame knot in  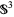satisfies

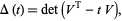(2)

where 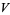 is a Seifert matrix, det is the determinant, and  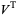denotes the transpose.

The Alexander polynomial is symmetric in 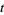 and 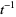 and satisfies

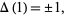(3)

where convention determines the sign. In this work, the convention 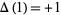 is used. The quantity  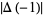is known at the knot determinant.

The notation 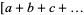 is an abbreviation for the Alexander polynomial of a knot

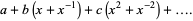(4)

The notation can also be extended for links, in which case one or more matrices is used to generate the corresponding multivariate Alexander polynomial (Rolfsen 1976, p. 389).

Let the Alexander polynomial of a link 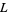 in the variable  be denoted 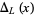. Then there exists a skein relationship discovered by J. H. Conway,

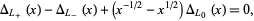(5)

corresponding to the above link diagrams (Adams 1994). This relation allows Alexander polynomials to be constructed for arbitrary knots by building them up as a sequence of over- and undercrossings.

The Alexander polynomial of a splittable link is always 0.

Surprisingly, there are known examples of nontrivial knots with Alexander polynomial 1, although no such examples occur among the knots of 10 or fewer crossings. An example is the 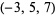-pretzel knot (Adams 1994, p. 167). Rolfsen (1976, p. 167) gives four other such examples.

A modified version of the Alexander polynomial was formulated by J. H. Conway. It is variously known as the Conway polynomial (Livingston 1993, pp. 207-215) or Conway-Alexander polynomial, and is denoted 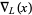. It is a reparametrization of the Alexander polynomial given by

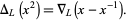(6)

The skein relationship convention used by for the Conway polynomial is

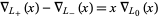(7)

(Doll and Hoste 1991).

Examples of Alexander 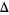 and Conway  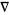polynomials for common knots are given in the following table

knot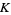
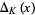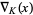trefoil knot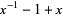
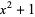figure eight knot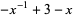
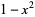Solomon's seal knot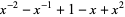
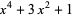stevedore's knot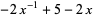
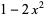Miller Institute knot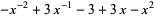

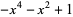For a knot,

{1 (mod 8) if Arf(K)=0; 5 (mod 8) if Arf(K)=1, " src="https://mathworld.wolfram.com/images/equations/AlexanderPolynomial/NumberedEquation8.gif" style="height:41px; width:218px" />

(8)

where Arf is the Arf invariant (Jones 1985).

The HOMFLY polynomial 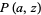 generalizes the Alexander polynomial (as well at the Jones polynomial) with

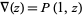(9)

(Doll and Hoste 1991).

Rolfsen (1976) gives a tabulation of Alexander polynomials 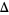 (in abbreviated notation) for knots up to 10 crossings and links up to 9 crossings. Livingston (1993) gives an explicit table of Alexander polynomials (with negative powers cleared and initial minus sign) for knots up to 9 crossings.

REFERENCES:

Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 165-169, 1994.

Alexander, J. W. "Topological Invariants of Knots and Links." Trans. Amer. Math. Soc. 30, 275-306, 1928.

Alexander, J. W. "A Lemma on a System of Knotted Curves." Proc. Nat. Acad. Sci. USA 9, 93-95, 1923.

Bar-Natan, D. "The Rolfsen Knot Table." https://www.math.toronto.edu/~drorbn/KAtlas/Knots/.

Casti, J. L. "The Alexander Polynomial." Ch. 1 in Five More Golden Rules: Knots, Codes, Chaos, and Other Great Theories of 20th-Century Mathematics. New York: Wiley, pp. 1-34, 2000.

Doll, H. and Hoste, J. "A Tabulation of Oriented Links." Math. Comput. 57, 747-761, 1991.

Jones, V. "A Polynomial Invariant for Knots via von Neumann Algebras." Bull. Amer. Math. Soc. 12, 103-111, 1985.

Livingston, C. "Alexander Polynomials." Appendix 2 in Knot Theory. Washington, DC: Math. Assoc. Amer., pp. 229-232, 1993.

Murasugi, K. and Kurpita, B. I. A Study of Braids. Dordrecht, Netherlands: Kluwer, 1999.

Rolfsen, D. "Table of Knots and Links." Appendix C in Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 280-287, 1976.

Stoimenow, A. "Alexander Polynomials." https://www.ms.u-tokyo.ac.jp/~stoimeno/ptab/a10.html.

Stoimenow, A. "Conway Polynomials." https://www.ms.u-tokyo.ac.jp/~stoimeno/ptab/c10.html.

اخر الاخبار

اخبار العتبة العباسية المقدسة

خمسون عامًا من العطاء.. نجم الأعرجي خادم الزائرين بلا انقطاع

العتبة العباسية المقدسة تواصل إقامة مجالسها العزائية لإحياء شهر المحرم

العتبة العباسية المقدسة تطلق سلسلة محاضرات قرآنية عاشورائية في بابل

في مساء اليوم الخامس من المحرّم.. المواكب الكربلائيّة تواصل فعالياتها العزائية

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد