
BLM/Ho Polynomial
 المؤلف:
Brandt, R. D.; Lickorish, W. B. R.; and Millett, K. C.
المؤلف:
Brandt, R. D.; Lickorish, W. B. R.; and Millett, K. C.
 المصدر:
"A Polynomial Invariant for Unoriented Knots and Links." Invent. Math. 84
المصدر:
"A Polynomial Invariant for Unoriented Knots and Links." Invent. Math. 84
 الجزء والصفحة:
...
الجزء والصفحة:
...
 12-6-2021
12-6-2021
 3017
3017
BLM/Ho Polynomial
A 1-variable unoriented knot polynomial 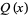 . It satisfies
. It satisfies
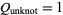 |
(1)
|
and the skein relationship
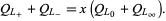 |
(2)
|
It also satisfies
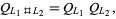 |
(3)
|
where 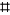 is the knot sum and
is the knot sum and
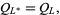 |
(4)
|
where 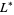 is the mirror image of
is the mirror image of 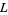 . The BLM/Ho polynomials of mutant knots are also identical. Brandt et al. (1986) give a number of interesting properties. For any link
. The BLM/Ho polynomials of mutant knots are also identical. Brandt et al. (1986) give a number of interesting properties. For any link 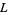 with
with 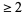 components,
components, 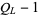 is divisible by
is divisible by 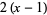 . If
. If 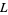 has
has 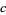 components, then the lowest power of
components, then the lowest power of  in
in 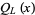 is
is 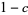 , and
, and
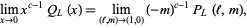 |
(5)
|
where 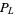 is the HOMFLY polynomial. Also, the degree of
is the HOMFLY polynomial. Also, the degree of 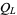 is less than the link crossing number of
is less than the link crossing number of 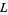 . If
. If 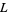 is a 2-bridge knot, then
is a 2-bridge knot, then
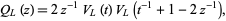 |
(6)
|
where 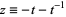 (Kanenobu and Sumi 1993).
(Kanenobu and Sumi 1993).
The polynomial was subsequently extended to the 2-variable Kauffman polynomial F, which satisfies
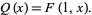 |
(7)
|
Brandt et al. (1986) give a listing of 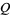 polynomials for knots up to 8 crossings and links up to 6 crossings.
polynomials for knots up to 8 crossings and links up to 6 crossings.
REFERENCES:
Brandt, R. D.; Lickorish, W. B. R.; and Millett, K. C. "A Polynomial Invariant for Unoriented Knots and Links." Invent. Math. 84, 563-573, 1986.
Ho, C. F. "A New Polynomial for Knots and Links--Preliminary Report." Abstracts Amer. Math. Soc. 6, 300, 1985.
Kanenobu, T. and Sumi, T. "Polynomial Invariants of 2-Bridge Knots through 22-Crossings." Math. Comput. 60, 771-778 and S17-S28, 1993.
Stoimenow, A. "Brandt-Lickorish-Millett-Ho Polynomials." http://www.ms.u-tokyo.ac.jp/~stoimeno/ptab/blmh10.html.
 الاكثر قراءة في التبلوجيا
الاكثر قراءة في التبلوجيا
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


