

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Jones Polynomial
المؤلف:
Adams, C. C.
المصدر:
The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, 1994.
الجزء والصفحة:
...
13-6-2021
5421
Jones Polynomial
The second knot polynomial discovered. Unlike the first-discovered Alexander polynomial, the Jones polynomial can sometimes distinguish handedness (as can its more powerful generalization, the HOMFLY polynomial). Jones polynomials are Laurent polynomials in 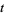 assigned to an
assigned to an 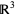 knot. The Jones polynomials are denoted
knot. The Jones polynomials are denoted 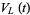 for links,
for links, 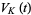 for knots, and normalized so that
for knots, and normalized so that
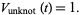 |
(1) |
For example, the right-hand and left-hand trefoil knots have polynomials
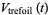 |
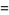 |
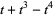 |
(2) |
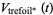 |
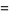 |
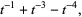 |
(3) |
respectively.
If a link has an odd number of components, then 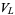 is a Laurent polynomial over the integers; if the number of components is even,
is a Laurent polynomial over the integers; if the number of components is even, 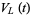 is
is 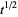 times a Laurent polynomial. The Jones polynomial of a knot sum
times a Laurent polynomial. The Jones polynomial of a knot sum 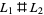 satisfies
satisfies
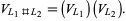 |
(4) |
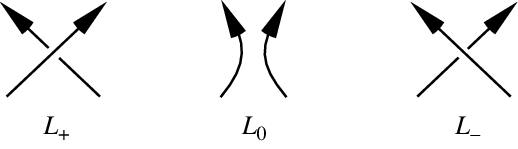
The skein relationship for under- and overcrossings is
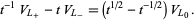 |
(5) |
Combined with the link sum relationship, this allows Jones polynomials to be built up from simple knots and links to more complicated ones.
Some interesting identities from Jones (1985) follow. For any link 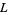 ,
,
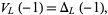 |
(6) |
where 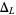 is the Alexander polynomial, and
is the Alexander polynomial, and
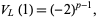 |
(7) |
where 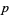 is the number of components of
is the number of components of 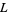 . For any knot
. For any knot 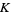 ,
,
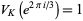 |
(8) |
and
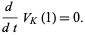 |
(9) |
Let 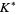 denote the mirror image of a knot
denote the mirror image of a knot 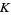 . Then
. Then
 |
(10) |
Jones defined a simplified trace invariant for knots by
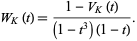 |
(11) |
The Arf invariant of 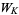 is given by
is given by
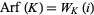 |
(12) |
(Jones 1985), where i is 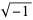 . A table of the
. A table of the 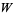 polynomials is given by Jones (1985) for knots of up to eight crossings, and by Jones (1987) for knots of up to 10 crossings. (Note that in these papers, an additional polynomial which Jones calls
polynomials is given by Jones (1985) for knots of up to eight crossings, and by Jones (1987) for knots of up to 10 crossings. (Note that in these papers, an additional polynomial which Jones calls 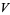 is also tabulated, but it is not the conventionally defined Jones polynomial.)
is also tabulated, but it is not the conventionally defined Jones polynomial.)
Jones polynomials were subsequently generalized to the two-variable HOMFLY polynomials, the relationship being
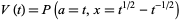 |
(13) |
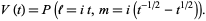 |
(14) |
They are related to the Kauffman polynomial F by
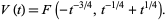 |
(15) |
Jones (1987) gives a table of braid words and 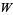 polynomials for knots up to 10 crossings. Jones polynomials for knots up to nine crossings are given in Adams (1994) and for oriented links up to nine crossings by Doll and Hoste (1991). All prime knots with 9 or fewer crossings have distinct Jones polynomials. However, there exist distinct knots (and even knots having different crossing numbers) that share the same Jones polynomial. Examples include (05-001, 10-132), (08-008, 10-129), (08-016, 10-156), (10-025, 10-056), (10-022, 10-035), (10-041, 10-094), (10-043, 10-091), (10-059, 10-106), (10-060, 10-083), (10-071, 10-104), (10-073, 10-086), (10-081, 10-109), and (10-137, 10-155) (Jones 1987). (Incidentally, the first four of these also have the same HOMFLY polynomial.)
polynomials for knots up to 10 crossings. Jones polynomials for knots up to nine crossings are given in Adams (1994) and for oriented links up to nine crossings by Doll and Hoste (1991). All prime knots with 9 or fewer crossings have distinct Jones polynomials. However, there exist distinct knots (and even knots having different crossing numbers) that share the same Jones polynomial. Examples include (05-001, 10-132), (08-008, 10-129), (08-016, 10-156), (10-025, 10-056), (10-022, 10-035), (10-041, 10-094), (10-043, 10-091), (10-059, 10-106), (10-060, 10-083), (10-071, 10-104), (10-073, 10-086), (10-081, 10-109), and (10-137, 10-155) (Jones 1987). (Incidentally, the first four of these also have the same HOMFLY polynomial.)
It is not known if there is a nontrivial knot with Jones polynomial 1.
The Jones polynomial of an 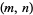 -torus knot is
-torus knot is
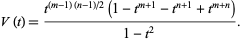 |
(16) |
Let 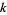 be one component of an oriented link
be one component of an oriented link 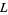 . Now form a new oriented link
. Now form a new oriented link 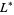 by reversing the orientation of
by reversing the orientation of 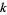 . Then
. Then
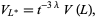 |
(17) |
where 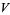 is the Jones polynomial and
is the Jones polynomial and 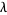 is the linking number of
is the linking number of 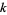 and
and 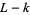 . No such result is known for HOMFLY polynomials (Lickorish and Millett 1988).
. No such result is known for HOMFLY polynomials (Lickorish and Millett 1988).
Birman and Lin (1993) showed that substituting the power series for 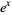 as the variable in the Jones polynomial yields a power series whose coefficients are Vassiliev invariants.
as the variable in the Jones polynomial yields a power series whose coefficients are Vassiliev invariants.
Let 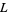 be an oriented connected link projection of
be an oriented connected link projection of 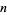 crossings, then
crossings, then
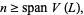 |
(18) |
with equality if 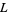 is alternating and has no reducible crossing (Lickorish and Millett 1988).
is alternating and has no reducible crossing (Lickorish and Millett 1988).
Witten (1989) gave a heuristic definition in terms of a topological quantum field theory, and Sawin (1996) showed that the "quantum group" 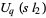 gives rise to the Jones polynomial.
gives rise to the Jones polynomial.
REFERENCES:
Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, 1994.
Birman, J. S. and Lin, X.-S. "Knot Polynomials and Vassiliev's Invariants." Invent. Math. 111, 225-270, 1993.
Doll, H. and Hoste, J. "A Tabulation of Oriented Links." Math. Comput. 57, 747-761, 1991.
El-Misiery, A. "An Algorithm for Calculating Jones Polynomials." Appl. Math. Comput. 74, 249-259, 1996.
Jones, V. "A Polynomial Invariant for Knots via von Neumann Algebras." Bull. Am. Math. Soc. 12, 103-111, 1985.
Jones, V. "Hecke Algebra Representations of Braid Groups and Link Polynomials." Ann. Math. 126, 335-388, 1987.
Khovanov, M. "A Categorification of the Jones Polynomial." 30 Aug 1999. https://arxiv.org/abs/math.QA/9908171.
Khovanov, M. "A Categorification of the Jones Polynomial." Duke Math. J. 101, 359-426, 2000.
Lickorish, W. B. R. and Millett, B. R. "The New Polynomial Invariants of Knots and Links." Math. Mag. 61, 1-23, 1988.
Murasugi, K. "Jones Polynomials and Classical Conjectures in Knot Theory." Topology 26, 297-307, 1987.
Murasugi, K. and Kurpita, B. I. A Study of Braids. Dordrecht, Netherlands: Kluwer, 1999.
Praslov, V. V. and Sossinsky, A. B. Knots, Links, Braids and 3-Manifolds: An Introduction to the New Invariants in Low-Dimensional Topology. Providence, RI: Amer. Math. Soc., 1996.
Sawin, S. "Links, Quantum Groups, and TQFTS." Bull. Amer. Math. Soc. 33, 413-445, 1996.
Stoimenow, A. "Jones Polynomials." https://www.ms.u-tokyo.ac.jp/~stoimeno/ptab/j10.html.
Thistlethwaite, M. "A Spanning Tree Expansion for the Jones Polynomial." Topology 26, 297-309, 1987.
Witten, E. "Quantum Field Theory and the Jones Polynomial." Comm. Math. Phys. 121, 351-399, 1989. https://projecteuclid.org/Dienst/UI/1.0/Summarize/euclid.cmp/1104178138.
 الاكثر قراءة في التبلوجيا
الاكثر قراءة في التبلوجيا
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















