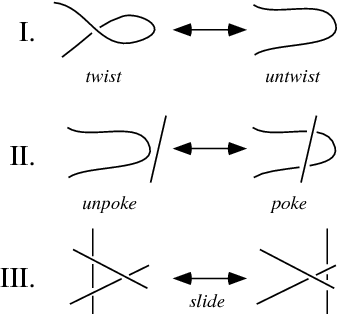
In the 1930s, Reidemeister first rigorously proved that knots exist which are distinct from the unknot. He did this by showing that all knot deformations can be reduced to a sequence of three types of "moves," called the (I) twist move, (II) poke move, and (III) slide move. These moves are most commonly called Reidemeister moves, although the term "equivalence moves" is sometimes also used (Aneziris 1999, p. 29).

Reidemeister's theorem guarantees that moves I, II, and III correspond to ambient isotopy (moves II and III alone correspond to regular isotopy). He then defined the concept of colorability, which is invariant under Reidemeister moves.

REFERENCES:

Aneziris, C. N. "The Equivalence Moves." Ch. 4 in The Mystery of Knots: Computer Programming for Knot Tabulation. Singapore: World Scientific, pp. 29-33, 1999.

Hoste, J.; Thistlethwaite, M.; and Weeks, J. "The First  Knots." Math. Intell. 20, 33-48, Fall 1998.

Kauffman, L. Knots and Physics. Teaneck, NJ: World Scientific, p. 16, 1991.

Reidemeister, K. "Knotten und Gruppen." Abh. Math. Sem. Univ. Hamburg 5, 7-23, 1927.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الفكرية ينظم ندوة عن الأبعاد الفكرية والعقدية لثورة الإمام الحسين (عليه السلام)

المجمع العلمي يواصل برامجه ودوراته القرآنية في عدد من المحافظات العراقية

لليوم الرابع.. قسم العلاقات العامة يواصل إقامة فعاليات مخيّم البذرة الواعدة

العتبة العباسية المقدسة تطلق التشغيل التجريبي لمعمل غسيل السجاد والأغطية

المزيد

الآخبار الصحية

نصائح عملية للحد من التعرق المفرط في الصيف

أطباء يحذرون: مكمل غذائي شائع قد يدمر الجهاز العصبي

تحذير طبي من تأثير جانبي "غير متوقع" لحقن التخسيس

حمامات الثلج قد تكون خطيرة وأحيانا مميتة.. ما السبب؟

المزيد

الآخبار التكنلوجية

أكبر جدارية شمسية في العالم تدخل موسوعة غينيس.. مشروع ضخم

تسارع دوران الأرض يثير القلق.. وتحذيرات من "كوارث محتملة" ؟

"سوذبيز" تطرح أكبر قطعة من المريخ على الأرض في مزاد علني

أوبن أيه آي تعتزم إطلاق متصفح إنترنت يعمل بالذكاء الاصطناعي

المزيد