Knot Group

Given a knot diagram, it is possible to construct a collection of variables and equations, and given such a collection, a group naturally arises that is known as the group of the knot. While the group itself depends on the choices made in the construction, any two groups that arise in this way are isomorphic (Livingston 1993, p. 103).

For example, the knot group of the trefoil knot is

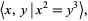(1)

or equivalently

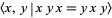(2)

(Rolfsen 1976, pp. 52 and 61), while that of Solomon's seal knot is

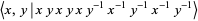(3)

(Livingston 1993, p. 127).

The group of a knot is not a complete knot invariant (Rolfsen 1976, p. 62). Furthermore, it is often quite difficult to prove that two knot group presentations represent nonisomorphic groups (Rolfsen 1976, p. 63).

REFERENCES:

Livingston, C. Knot Theory. Washington, DC: Math. Assoc. Amer., 1993.

Rolfsen, D. "The Knot Group." §3B in Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 51-52, 1976.