


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-6-2017
Date: 2-7-2017
Date: 6-7-2021
|
Conway's knot is the prime knot on 11 crossings with braid word
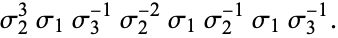 |
The Jones polynomial of Conway's knot is
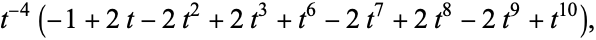 |
which is the same as for the Kinoshita-Terasaka knot.
Conway's knot is not a slice knot (Delbert 2020, Klarreich 2020, Piccirillo 2020).
REFERENCES:
Conway, J. H. "An Enumeration of Knots and Links." In Computational Problems in Abstract Algebra (Ed. J. Leech). Oxford, England: Pergamon Press, pp. 329-358, 1970.
Cromwell, P. Knots and Links. Cambridge, England: Cambridge University Press, pp. 180-181, 2004.
Delbert, C. "Young Mathematician Solves Old, Famous Knot Problem in Barely a Week." Popular Mechanics. May 22, 2020. https://www.popularmechanics.com/science/a32635156/conway-knot-problem-solved/.
Klarreich, E. "A Grad Student Solved the Epic Conway Knot Problem--in a Week." Quanta. May 19, 2020. https://www.quantamagazine.org/graduate-student-solves-decades-old-conway-knot-problem-20200519/.
Montesinos, J. "Surgery on Links and Double Branched Covers of 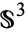 ." In Knots, Groups, and 3-Manifolds: Papers dedicated to the memory of R. H. Fox (Ed. L. P. Neuwerth). Princeton, NJ: Princeton University Press, pp. 227-259, 1975.
." In Knots, Groups, and 3-Manifolds: Papers dedicated to the memory of R. H. Fox (Ed. L. P. Neuwerth). Princeton, NJ: Princeton University Press, pp. 227-259, 1975.
Piccirillo, L. "The Conway Knot Is Not Slice." Ann. Math. 191, 581-591, 2020.
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, p. 173, 1976.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تستعدّ لتكريم عددٍ من الطالبات المرتديات للعباءة الزينبية في جامعات كركوك
|
|
|