A codimension one foliation 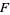 of a 3-manifold  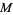is said to be taut if for every leaf  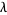in the leaf space  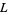of 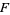, there is a circle  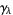transverse to  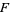(i.e., a closed loop transverse to the tangent field of 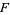) which intersects .

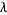Taut foliations play a significant role in various aspects of topology and are credited as being one of two major tools (along with incompressible surfaces) responsible for revealing significant topological and geometric information about 3-manifolds (Gabai and Oertel 1989). As such, a considerable amount of research has gone into the study of taut foliations on 3-manifolds. One well-known result is that every taut foliation is necessarily Reebless and that, for any non-taut Reebless foliation, the leaves which don't admit a closed transversal are necessarily tori. Additionally, the closed leaves of a taut foliation are homologically nontrivial.

Some classification results for taut foliations are also known. One such result, attributed by Eliashberg and Thurston to Novikov and Sullivan, says that a foliation 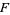 on a closed 3-manifold  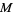is taut if it is different from the foliati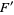on  on 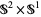 and satisfies any one of the following:

1. Each lea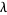f  of 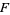 is intersected by a transversal closed curve.

2. There exists a vector field 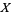 on 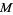 which is transversal to  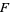and preserves a volume form  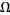on .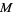

3. 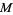 admits a Riemannian metric for which all leaves are minimal surfaces.

Moreover, a necessary and sufficient condition for tautness of a foliation 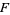 is that  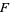contain no generalized Reeb components (Goodman 1975).

REFERENCES:

Calegari, D. Foliations and the Geometry of 3-Manifolds. Oxford, England: Clarendon Press, 2007.

Eliashberg, Y. M. and Thurston, W. P. Confoliations. Providence, RI: Amer. Math. Soc., 1998.

Gabai, D. and Oertel, U. "Essential Laminations in 3-Manifolds." Ann. Math. 130, 41-73, 1989.

Goodman, S. "Closed Leaves in Foliations of Codimension One." Comm. Math. Helv. 50, 383-388, 1975.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الدينية يوزع أكثر من ألفي وجبة طعام للمعزين في ذكرى عاشوراء بنينوى

قسم الشؤون الطبية يواصل تقديم خدماته الصحية لزائري عاشوراء

جموع المعزين تحيي مراسم يوم العاشر من شهر المحرم عند المرقدين الطاهرين

قسم العلاقات يطلق محطات فتية الكفيل الثقافية في محافظة نينوى

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد