First Category

A subset 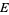 of a topological space  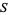is said to be of first category in  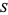if 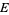 can be written as the countable union of subsets which are nowhere dense in 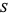, i.e., if  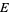is expressible as a union

where each subset 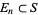 is nowhere dense in 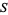. Informally, one thinks of a first category subset as a "small" subset of the host space and indeed, sets of first category are sometimes referred to as meager. Sets which are not of first category are of second category.

An important distinction should be made between the above-used notion of "category" and category theory. Indeed, the notions of first and second category sets are independent of category theory.

The rational numbers are of first category and the irrational numbers are of second category in 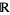 with the usual topology. In general, the host space and its topology play a fundamental role in determining category. For example, the set  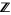of integers with the subset topology inherited from  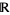is (vacuously) of second category relative to itself because every subset of  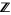is open in  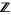with respect to that topology; on the other hand,  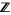is of first category in  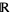with its standard topology and in  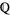with the subset topology inherited by  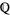from 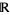. Likewise, the Cantor set is a Baire space (i.e., each of its open sets are of second category relative to it) even though it is of first category in the interval  with the usual topology.

REFERENCES:

Hocking, J. and Young, G. Topology. New York: Dover, p. 89, 1961.

Morgan, J. C. Point Set Theory. Boca Raton, FL: CRC Press, p. 21, 1989.

Munkres, J. R. Topology: A First Course. Upper Saddle River, NJ: Prentice-Hall, pp. 293-294, 1975.

Rudin, W. Functional Analysis. New York: McGraw-Hill, 1991.