Real Projective Plane

The real projective plane is the closed topological manifold, denoted 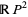, that is obtained by projecting the points of a plane  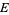from a fixed point  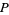(not on the plane), with the addition of the line at infinity. It can be described by connecting the sides of a square in the orientations illustrated above (Gardner 1971, pp. 15-17; Gray 1997, pp. 323-324).

There is then a one-to-one correspondence between points in 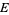 and lines through  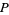not parallel to 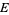. Lines through  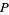that are parallel to  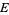have a one-to-one correspondence with points on the line at infinity. Since each line through  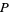intersects the sphere  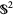centered at  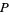and tangent to  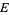in two antipodal points,  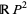can be described as a quotient space of  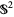by identifying any two such points. The real projective plane is a nonorientable surface. The equator of  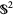(which, in the quotient space, is itself a projective line) corresponds to the line at infinity.

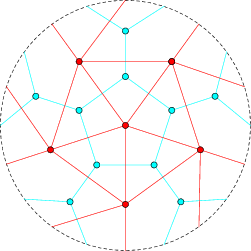
The complete graph on 6 vertices 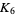 can be drawn in the projective plane without any lines crossing, as illustrated above. Here, the projective plane is shown as a dashed circle, where lines continue on the opposite side of the circle. The dual of  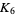on the projective plane is the Petersen graph.

The Boy surface, cross-cap, and Roman surface are all homeomorphic to the real projective plane and, because 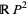 is nonorientable, these surfaces contain self-intersections (Kuiper 1961, Pinkall 1986).

REFERENCES:

Apéry, F. Models of the Real Projective Plane: Computer Graphics of Steiner and Boy Surfaces. Braunschweig, Germany: Vieweg, 1987.

Coxeter, H. S. M. The Real Projective Plane, 3rd ed. Cambridge, England: Cambridge University Press, 1993.

Gardner, M. Martin Gardner's Sixth Book of Mathematical Games from Scientific American. New York: Scribner's, 1971.

Geometry Center. "The Projective Plane." https://www.geom.umn.edu/zoo/toptype/pplane/.

Gray, A. "Realizations of the Real Projective Plane." §14.6 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 330-335, 1997.

Klein, F. §1.2 in Vorlesungen über nicht-euklidische Geometrie. New York: Springer-Verlag, 1968.

Kuiper, N. H. "Convex Immersion of Closed Surfaces in 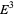." Comment. Math. Helv. 35, 85-92, 1961.

Pinkall, U. Mathematical Models from the Collections of Universities and Museums (Ed. G. Fischer). Braunschweig, Germany: Vieweg, pp. 64-65, 1986.