


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-9-2021
Date: 29-11-2021
Date: 19-9-2021
|
The equations defined by
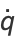 |
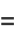 |
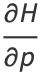 |
(1) |
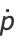 |
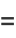 |
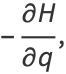 |
(2) |
where 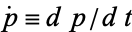 and
and 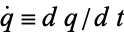 is fluxion notation and
is fluxion notation and 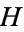 is the so-called Hamiltonian, are called Hamilton's equations. These equations frequently arise in problems of celestial mechanics.
is the so-called Hamiltonian, are called Hamilton's equations. These equations frequently arise in problems of celestial mechanics.
The vector form of these equations is
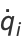 |
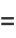 |
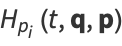 |
(3) |
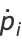 |
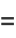 |
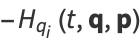 |
(4) |
(Zwillinger 1997, p. 136; Iyanaga and Kawada 1980, p. 1005).
Another formulation related to Hamilton's equation is
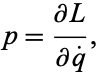 |
(5) |
where 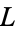 is the so-called Lagrangian.
is the so-called Lagrangian.
REFERENCES:
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1005, 1980.
Morse, P. M. and Feshbach, H. "Hamilton's Principle and Classical Dynamics." §3.2 in Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 280-301, 1953.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, 1997.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
الزائرون يحيون ليلة الجمعة عند مرقد أبي الفضل العباس (عليه السلام)
|
|
|