


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
أقرأ أيضاً
التاريخ: 23-8-2018
التاريخ: 9-11-2021
التاريخ: 30-3-2019
التاريخ: 31-10-2021
|
الدالة الفردية : Odd Function
هي الدالة التي تحقق لكل قيم المتغير في المجال الخاصية :
F(-x) = - f(x)
وتسمى الدالة التي لها هذه الخاصية بالدالة الفردية .
مثال : لدينا الدالة :
F(x) = x3
مثل الاقتران بيانياً.
الحل:
نمثل الاقتران بيانياً على المستوى الديكارتي بتكوين جدول لبعض قيم (y) المناظرة.

ثم نقوم بتعيين النقاط في الجدول السابق على المستوى الديكارتي ، ونرسم منحنى الدالة ـ، وتسمى الدالة التي لها هذه الصيغة بالدالة الفردية. انظر إلى الشكل التالي.
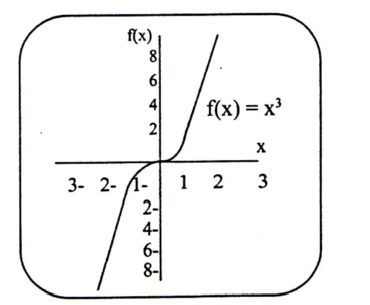
شكل (1-2)
منحنى الدالة الفردية يكون متماثلاً حول نقطة الأصل والعكس صحيح ، بمعنى ، أن كل دالة متماثل حول نقطة الأصل يكون فردياً.
ملاحظة مهمة : ليس بالضرورة أن تكون الدالة زوجية أو فردية ، حيث إن الكثير من الدوال ليست زوجية وليست فردية.
ملاحظة : بعدما مثلنا هذه الدوال الواردة في الأمثلة والتي هي كلها من عائلة كثيرات الحدود ، ننتقل الآن إلى نوع آخر من الدوال، وهي الدوال الكسرية.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|