


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-9-2021
Date: 30-11-2021
Date: 11-2-2016
|
Adams' method is a numerical method for solving linear first-order ordinary differential equations of the form
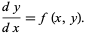 |
(1) |
Let
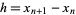 |
(2) |
be the step interval, and consider the Maclaurin series of 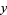 about
about 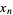 ,
,
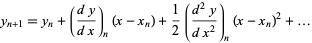 |
(3) |
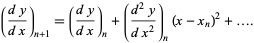 |
(4) |
Here, the derivatives of 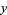 are given by the backward differences
are given by the backward differences
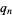 |
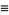 |
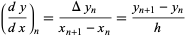 |
(5) |
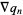 |
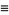 |
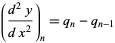 |
(6) |
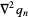 |
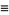 |
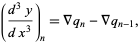 |
(7) |
etc. Note that by (◇), 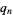 is just the value of
is just the value of 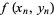 .
.
For first-order interpolation, the method proceeds by iterating the expression
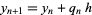 |
(8) |
where 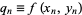 . The method can then be extended to arbitrary order using the finite difference integration formula from Beyer (1987)
. The method can then be extended to arbitrary order using the finite difference integration formula from Beyer (1987)
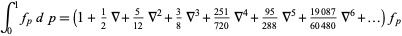 |
(9) |
to obtain
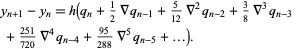 |
(10) |
Note that von Kármán and Biot (1940) confusingly use the symbol normally used for forward differences 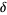 to denote backward differences
to denote backward differences 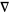 .
.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 896, 1972.
Bashforth, F. and Adams, J. C. Theories of Capillary Action. London: Cambridge University Press, 1883.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 455, 1987.
Jeffreys, H. and Jeffreys, B. S. "The Adams-Bashforth Method." §9.11 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 292-293, 1988.
Kármán, T. von and Biot, M. A. Mathematical Methods in Engineering: An Introduction to the Mathematical Treatment of Engineering Problems. New York: McGraw-Hill, pp. 14-20, 1940.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, p. 741, 1992.
Whittaker, E. T. and Robinson, G. "The Numerical Solution of Differential Equations." Ch. 14 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 363-367, 1967.



|
|
|
|
لشعر لامع وكثيف وصحي.. وصفة تكشف "سرا آسيويا" قديما
|
|
|
|
|
|
|
كيفية الحفاظ على فرامل السيارة لضمان الأمان المثالي
|
|
|
|
|
|
|
شعبة مدارس الكفيل: مخيَّم بنات العقيدة يعزِّز القيم الدينية وينمِّي مهارات اتخاذ القرار لدى المتطوِّعات
|
|
|