
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-11-2021
Date: 21-11-2021
Date: 21-8-2021
|
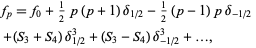 |
(1) |
for ![p in [-1/2,1/2]](https://mathworld.wolfram.com/images/equations/SteffensonsFormula/Inline1.gif) , where
, where 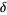 is the central difference and
is the central difference and
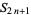 |
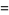 |
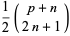 |
(2) |
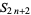 |
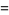 |
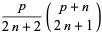 |
(3) |
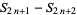 |
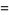 |
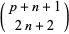 |
(4) |
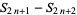 |
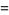 |
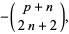 |
(5) |
where 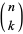 is a binomial coefficient.
is a binomial coefficient.
REFERENCES:
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 433, 1987.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
الأمانة العامة للعتبة الكاظمية المقدسة تستضيف مؤتمر أبناء الإمام الرضا الدولي الرابع
|
|
|