


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2024-01-23
التاريخ: 21-3-2021
التاريخ: 23-3-2017
التاريخ: 28-3-2021
|
بالعودة إلى العقد الأول من القرن العشرين، عندما كان رذرفورد وزميله فردريك سودي يفحصان طبيعة النشاط الإشعاعي، اكتشفا خاصية مثيرة وأساسية من خصائص الذرة، أو بالأحرى من خصائص نواة الذرة. لا بد أن يتضمن «التحلل» الإشعاعي، كما أصبح معروفا بهذا الاسم، تغيرا أساسيا في الذرة المفردة (معلوم لدينا الآن أنه يتضمن انشطار النواة وانطلاق أجزاء منها)، غير أنه فيما يبدو لا يتأثر بأي ٍ مؤثر خارجي. فسواء جرى تسخين الذرات أو تبريدها، وسواء وضعت في فراغ أو في دلو به ماء، فإن التحلل الاشعاعي سيستمر دون أي مقاطعة. ويبدو أنه لا توجد طريقة للتنبؤ الدقيق بأن ذرةً بعينها في مادة ٍ مشعة ما ستتحلل، وتبعث بجسيم ألفا أو بيتا وبأشعة جاما، إلا أن التجارب قد بيَّنت أن نسبةً معينة من عدد كبير من الذرات النشطة إشعاعيا للعنصر نفسه ستتحلل دائما في زمن معين. وعلى وجه التحديد، يوجد زمن مميز لكل عنصر مشع يسمى عمر النصف، تتحلل خلاله أنصاف الذرات بالضبط في أي نموذج تحلل. يبلغ عمر النصف لعنصر راديوم، على سبيل المثال، ٦٠٠ سنة، بينما يبلغ عمر النصف لعنصر الكربون-١٤ — وهو أحد نظائر الكربون المشعة — أقل قليلا من ٦٠٠٠ سنة، وهو ما جعله مفيدا في التأريخ الزمني للاكتشافات الأثرية، وأخيرا يبلغ عمر النصف لتحلل عنصر البوتاسيوم المشع ١٣٠٠ مليون سنة. ومن دون معرفة السبب الذي يجعل ذرة ما ضمن عدد هائل من الذرات تتحلَّل ولا تتحلل الذرات المجاورة لها، استخدم رذرفورد وسودي هذا الاكتشاف كأساس لوضع ٍ نظرية إحصائية عن التحلل الإشعاعي، وهي نظرية تَستخدم أساليب أكتوارية كالمطبقة في شركات التأمين، التي تعرف أن بعض الأشخاص المؤمن عليهم سيموتون في سن مبكرة ِ وأن ورثتهم سيتسلمون من شركة َ التأمين مبالغ تفوق كثيرا ما دفعوه، في حين أن عملاء آخرين سيعيشون طويلا وسيدفعون مبالغ كافية لتعويض ذلك. ودون معرفة الوقت الذي سيموت فيه أي من العملاء، تتيح الجداول الأكتوارية لموظفي الحسابات ضبط الموازنة. وبالطريقة نفسها، تتيح الجداول الإحصائية للفيزيائيين ضبط موازنة التحلل الإشعاعي، بشرط أن يتعاملوا مع مجموعات كبيرة من الذرات. إحدى السمات اللافتة لهذا السلوك هي أن النشاط الإشعاعي لا يختفي أبدا من عينة أي مادة مشعة. ذلك حيث يتحلل نصف ملايين الذرات الموجودة في فترة ٍ زمنية معينة. وعلى مدى عمر النصف التالي — الذي يستغرق الفترةَ الزمنية نفسها — سيتحلَّل نصف العدد المتبقي، وهكذا. وكلما اقتربنا من الصفر تناقص عدد الذرات المشعة المتبقية دون تحلل ولكن كل خطوة نحو الصفر تقلِّل عمر النصف بما يتناسب مع نصف العدد المتبقي.
في تلك الأيام الأولى، كان الفيزيائيون من أمثال رذرفورد وسودي يتصورون أن شخصا ما سيأتي في النهاية ويكتشف بالضبط السبب وراء تحلل ذرة بعينها، وأن هذا لاكتشاف سيفسر الطبيعة الإحصائية للعملية. وعندما طبق أينشتاين الأساليب الإحصائية على نموذج بور لتفسيرِ تفاصيل الطيف الذري، استبق الأمر أيضا بأن الاكتشافات اللاحقة ستلغي الحاجة إلى «الجداول الأكتوارية». وكانوا جميعا على خطأ. يمكن النظر إلى مستويات الطاقة للذرة، أو للإلكترون في ذرة ما، على أنها درجات ُسلَم. ولا يتساوى عمق كل درجة والأخرى من حيث الطاقة؛ فالدرجات العلوية تكون متقاربة َ بعضها من بعض أكثر من الدرجات السفلية. وقد أوضح بور أنه في حالة ذرة الهيدروجين، بوصفها أبسط الذرات، يمكن تمثيل مستويات الطاقة كدرجات سلم بحيث يتناسب عمق كل درجة أسفل أعلى الدرج مع 1/n^2؛ حيث n هو رقم كل درجة بدءًا من أسفل الدرج. ويتطلب انتقال إلكترون من المستوى واحد إلى المستوى اثنين على هذا الدرج
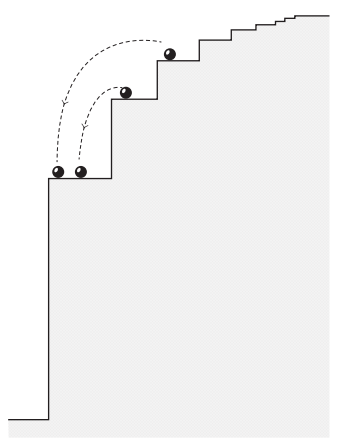
شكل 4-1: ٍ يمكن مقارنة مستويات الطاقة في ذرة بسيطة مثل الهيدروجين بمجموعة من درجات السلم ذات أعماق مختلفة. تمثل الكرة الموضوعة على الدرجات المختلفة إلكترونًا في مستويات الطاقة المختلفة في الذرة. وتقابل الحركة من درجة أعلى إلى درجة أدنى انطلاق كمية محددة من الطاقة، وهي المسؤولة في ذرة الهيدروجين عن خطوط سلسلة بالمر في الطيف. ولا توجد خطوط بينية؛ لأنه ليس ثمة درجات بينية لكي «يستقر» عليها الإلكترون.
كمية من الطاقة مقدارها hν بالضبط ليتحرك أعلى هذه الدرجة من درجات السلَّم، وإذا عاد الإلكترون ليهبط إلى المستوى الأول («الحالة الأرضية» للذرة)، فإنه يطلق الكمية نفسها من الطاقة. ولا توجد وسيلة تجعل الإلكترون في الحالة الأرضية يمتص طاقة أقل؛ لأنه لا توجد «درجة» بينية يستطيع الإلكترون أن يستقر عليها، ولا توجد وسيلة تجعل إلكترونا في المستوى اثنين يطلق مقدارا أقل من هذه الكمية من الطاقة؛ لأنه لا يوجد موضع آخر ليهبط إليه الإلكترون سوى الحالة الأرضية. ونظرا لوجود العديد من الدرجات التي يمكن للإلكترون الاستقرار عليها، ولأنه يستطيع القفز أو الهبوط من أي درجة إلى أي درجة أخرى، يوجد العديد من الخطوط في طيف كل عنصر. وكل خط منها يقابل انتقالا بين درجتين، بين مستويين للطاقة لهما أرقام كمية مختلفة. وتؤدي كل ٍ الانتقالات التي تنتهي بالحالة الأرضية، على سبيل المثال، إلى مجموعة من خطوط الطيف ِ على غرار سلسلة بالمر، وتؤدي كل الانتقالات من الدرجات الأعلى التي تنتهي في المستوى اثنين إلى مجموعة أخرى من الخطوط، وهكذا. (5) تتصادم الذرات في حالة الغاز الساخن باستمرار بعضها مع بعض، وبذلك تثار الإلكترونات إلى مستويات أعلى من الطاقة ثم تعود لتهبط من جديد، وفي أثناء ذلك تشع خطوط طيف براقة. أما عندما يمر الضوء َ خلال غاز بارد، فإن الإلكترونات في الحالة الأرضية ترتفع إلى مستويات طاقة أعلى، وفي أثناء ذلك تمتص الضوء تاركة خطوطا معتمة في الطيف.
وعلى افتراض أن نموذج الذرة لدى بور كان يعني شيئًا على أية حال، فإن هذا ِ التفسير لكيفية إشعاع الذرات الساخنة للطاقة كان ينبغي حتما ربطه بقانون بلانك. ولكان ينبغي حتما أن يكون طيف إشعاع التجويف (إشعاع الجسم الأسود) ببساطة ٍ هو التأثير المشترك لأعداد كبيرة من الذرات التي تشع طاقة كلما قفزت الإلكترونات من مستوى طاقة إلى آخر.
أكمل أينشتاين نظريته عن النسبية العامة سنة ١٩١٦، ووجه اهتمامه مجددا إلى نظرية الكم (قد يبدو ذلك تجديدا أو إحياء من جديد مقارنةً ببحثه الرئيسي). ولعل ما حمسه لذلك هو النجاح الذي حققه نموذج بور للذرة، وكذلك نسخته الخاصة في ذلك الوقت من النظرية الجسيمية للضوء التي بدأت أخيرا تكسب أرضا وتحوز شيوعا وتقدما. كان الفيزيائي الأمريكي أندرو ميليكان واحدا من أشد المعارضين لتفسير أينشتاين للظاهرة الكهروضوئية، عندما ظهر هذا التفسير لأول مرة سنة ١٩٠٥. وقد استغرق عشر ِ سنوات في اختبار ِ الفكرة من خلال سلسلة من التجارب المميزة، انطلاقًا من هدفه في إثبات خطأ أينشتاين وانتهاءً بالإثبات الذي توصل إليه سنة ١٩١٤ عن طريق ِ التجربة المباشرة بصحة تفسير أينشتاين للظاهرة الكهروضوئية بمدلول الكم الضوئي، أو الفوتون. وفي أثناء ذلك، استنتج طريقة تجريبية لتحديد قيمة h بدقة، واكتمالا للمفارقة حصل سنة ١٩٢٣ على جائزة نوبل عن أبحاثه وقياسه لشحنة الإلكترون. أدرك أينشتاين أن تحول ذرة من حالة طاقة «مثارة» — يوجد فيها الإلكترون ٍ في مستوى طاقة عال ٍ — إلى حالة ذات طاقة أقل — يوجد فيها الإلكترون في مستوى طاقة منخفض — يشبه كثيرا التحلل الإشعاعي للذرة. وقد استخدم الأساليب الإحصائية التي طورها بولتزمان (للتعامل مع سلوك مجموعات من الذرات) للتعامل مع حالات الطاقة المفردة، حيث توصل إلى حساب ِ احتمال ِ وجود ذرة معينة في حالة طاقة تقابل عددا كموميا معينا n ، واستخدم «جداول التأمين الأكتوارية» الاحتمالية للنشاط الإشعاعي لحساب احتمال «تفكك» ذرة ما في الحالة n أو «تحللها» إلى حالة أخرى ذات طاقة أقل (أي ذات عدد كمومي أقل). وقد أدى ذلك ببساطة ووضوح إلى معادلة بلانك لإشعاع ِ الجسم الأسود التي اشتقت بأكملها على أساس أفكار الكم. وفي فترة قريبة من ذلك، تمكن بور باستخدام أفكار أينشتاين الإحصائية من توسيع نطاق نموذجه الذري، مقرا ً بالتفسير القائل بأن بعض الخطوط في الطيف تكون أكثر وضوحا من غيرها لأن بعض الانتقالات بين حالات الطاقة تكون احتمالية — أرجحية — حدوثها أكبر من غيرها. ولم يستطع تفسير السبب وراء ذلك، غير أن أحدا لم يُول اهتماما كبيرا بالأمر في ذلك الوقت. كان أينشتاين، مثله مثل العلماء الذين درسوا النشاط الإشعاعي في ذلك الوقت، يعتقد أن الجداول الأكتوارية ليست كلمة الفَصل الأخيرة، وأن الأبحاث القادمة ستحدد السبب وراء حدوث انتقال بعينِه في اللحظة التي يحدث فيها بالضبط، وليس في أي وقت آخر. غري أن هذه هي النقطة التي بدأت عندها نظرية الكم تتحرر فعليا من سيطرة الأفكار الكلاسيكية، ولم يُكتشف قط أي «سبب كامن» وراء حدوث التحلل الاشعاعي أو انتقالات الطاقة الذرية حال حدوثها. وفي الواقع، يبدو أن هذه التغيرات تحدث كلها بمحض المصادفة، على أساس إحصائي ما، وقد بدأ ذلك الأمر في إثارة تساؤلات فلسفية جوهرية.
في العالم الكلاسيكي لكل شيء سبب. ويمكنك تتبع سبب أي حدث بتسلسل زمني عكسي لاكتشاف السبب وراء ذلك السبب، والسبب الذي أدى إلى ذلك السبب، وهكذا حتى تصل إلى الانفجار العظيم، أو حتى لحظة الخلْق في السياق الديني، إذا كان ذلك هو النموذج الذي تقبل به. أما في عالم الكم، فإن هذه السببية المباشرة ِ تأخذ في الاختفاء بمجرد فحص التحلل الإشعاعي والانتقالات الذرية. فالإلكترون لا يهبط من مستوى معين للطاقة إلى مستوى آخر في زمن معين لأي سبب محدد. ومستوى الطاقة الأدنى هو الأكثر تفضيلا َّ لدى الذرة، بالمفهوم الإحصائي، ولذا فمن المرجح (يمكن قياس مقدار الأرجحية كميا) أن يقوم الإلكترون بهذا الانتقال آجلا ً أو عاجلا. ولكن لا توجد وسيلة تخبرنا متى سيحدث هذا الانتقال. فلا يوجد عامل خارجي يدفع الإلكترون، ولا يوجد توقيت داخلي يفرض على الإلكترون القفز في توقيت َمحدد. وكل ما هنالك أن الانتقال يحدث في هذا الحين وليس ذاك دون سبب معين.
هوامش
(5) In fact, the Balmer series in hydrogen’s spectrum does correspond to the transitions that end on level two.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|