إن فكرة انحناء المكان أو تقوسه عَصِيَّة للغاية على الاستيعاب، لدرجة أن الفيزيائيين لا يحبون في الواقع تصور الأمر ذهنيًّا. ففَهمنا للخصائص الهندسية لعالمنا الطبيعي مبني على ما تحقق من إنجازات على يد أجيال من الرياضيين الإغريق، ومن أبرزها نظام إقليدس الشكلي الذي يضم أشياء على غرار نظرية فيثاغورس ومفهوم أن الخطوط المتوازية لا تتقاطع وأن مجموع الزوايا الداخلية للمثلث يساوي 180 درجة، وما إلى ذلك. كل هذه القواعد جزء من صرح الهندسة الإقليدية. لكن هذه القوانين والنظريات ليست محض رياضيات مجردة. فنحن نعلم من واقع خبرتنا اليومية أنها تصف خواص العالم المادي على نحو طيب للغاية. إن قوانين إقليدس تُستخدم كل يوم من جانب المعماريين والمساحين والمصممين ورسامي الخرائط؛ أي فعليًّا من جانب كل شخص ذي علاقة بخواص شكل المكان وموضع الأجسام فيه. فالهندسة علم واقعي ملموس.
ومِن ثَمَّ، يبدو من البديهي أن هذه الخواص المكانية التي تشربناها منذ الصغر ينبغي أن تنطبق على ما يتجاوز نطاق مبانينا والأراضي التي نمسحها. فمن المفترض أن تنطبق على الكون إجمالًا. ولا بد أن قوانين إقليدس جزء لا يتجزأ من نسيج العالم نفسه. أم الأمرُ خلاف ذلك؟ لكن رغم أن قوانين إقليدس تتّسم بالأناقة الرياضية والإقناع المنطقي، فإنها ليست المجموعة الوحيدة من القواعد التي يمكن أن تشيد نظاما هندسيا. وقد أدرك رياضيون من القرن التاسع عشر، على غرار جاوس وريمان، أن قوانين إقليدس تمثل فقط حالة خاصة من الهندسة يكون فيها سطح المكان منبسطا. ومن الممكن تشييد أنظمة أخرى يتم فيها خرق هذه القوانين.
فكّر، على سبيل المثال، في مثلث مرسوم على ورقة منبسطة. تنطبق نظريات إقليدس على هذه الحالة، وبذا يجب أن يساوي مجموع الزوايا الداخلية للمثلث 180 درجة (أي ما يعادل مجموع زاويتين قائمتين). لكن فكّر الآن فيما سيحدث إذا رسمت مثلثًا على سطح كرة. فمن الممكن أن ترسم. مثلثًا على سطح كرة يكون به ثلاث زوايا قائمة. على سبيل المثال، ارسم نقطة عند «القطب الشمالي» ونقطتين عند «خط الاستواء» يفصلهما مساحة تعادل ربع محيط الكرة. هذه النقاط الثلاث تشكّل مثلثا ذا ثلاث زوايا قائمة يخالف الهندسة الإقليدية.
هذا النوع من التفكير يصلح على نحو طيب بالنسبة إلى الهندسة ثنائية الأبعاد، لكن عالمنا له ثلاثة أبعاد مكانية. وتخيلُ مكانٍ منحَنِ ثلاثي الأبعاد أمر أكثر صعوبة بكثير. لكن على أي حال من الخطأ على الأرجح التفكير في «المكان» من الأساس. فعلى أي حال، لا يمكننا قياس المكان. بل ما يمكننا قياسه هو المسافات بين الأجسام الواقعة داخل المكان باستخدام المساطر أو، على نحو أكثر واقعية في السياق الفلكي، أشعة الضوء. إن التفكير في المكان بوصفه قطعة ورق منبسطة أو منحنية يشجعنا على التفكير فيه بوصفه شيئًا ملموسًا في حد ذاته، بدلًا من كونه الموضع الذي توجد فيه كل الأشياء الملموسة. وقد حاول أينشتاين دائمًا أن يتجنب التعامل مع كيانات على غرار «المكان» يكون توصيفها كَفِئَة في الوجود غير واضح. وقد كان يفضل أن يفكر بدلا من ذلك فيما يمكن أن يتوقع الراصد قياسه في أي تجربة بعينها.
احتذاء بهذا المنظور، يمكننا أن نسأل أنفسنا عن المسار الذي ستتخذه أشعة الضوء وفقًا لنظرية النسبية العامة. في الهندسة الإقليدية ينتقل الضوء في خطوط مستقيمة. وبإمكاننا أن نعتبر انتقال الضوء في خطوط مستقيمة يعني بالأساس أن المكان منبسط. في النسبية الخاصة، ينتقل الضوء في خطوط مستقيمة؛ لذا يكون المكان منبسطا وفق هذه النظرة للعالم. لكن تذكَّر أن النسبية العامة تنطبق على الحركة المتسارعة، أو الحركة في وجود تأثيرات جاذبية. فما الذي سيحدث للضوء في هذه الحالة؟
دعونا نَعُدْ إلى التجربة الفكرية التي تتضمن المصعد. وبدلا من وجود زنبرك معلق في طرفه ثقل، يكون المصعد الآن مزودًا بأداة تطلق شعاعًا من الليزر ينطلق من أحد جوانبه إلى الجانب المقابل له. المصعد موجود في أعماق الفضاء، بعيدًا عن أي جاذبية. إذا كان المصعد ساكنًا، أو يتحرك بسرعة ثابتة، فإن شعاع الضوء المنطلق سيرتطم بالنقطة المقابلة تمامًا للأداة التي أطلقت شعاع الليزر. هذا هو التنبؤ الذي تخرج به النسبية الخاصة. لكن تخيل الآن أن المصعد مثبت إليه صاروخ وأن تشغيل الصاروخ سيدفع المصعد إلى التسارع إلى الأعلى. الراصد الساكن الموجود خارج المصعد سيرى هذا المصعد وهو يتسارع في الحركة، لكن إذا رأى شعاع الليزر من الخارج فسيظل في نظره مستقيما بالمثل على الجانب الآخر، سيلاحظ الفيزيائي الموجود داخل المصعد شيئًا غريبا.
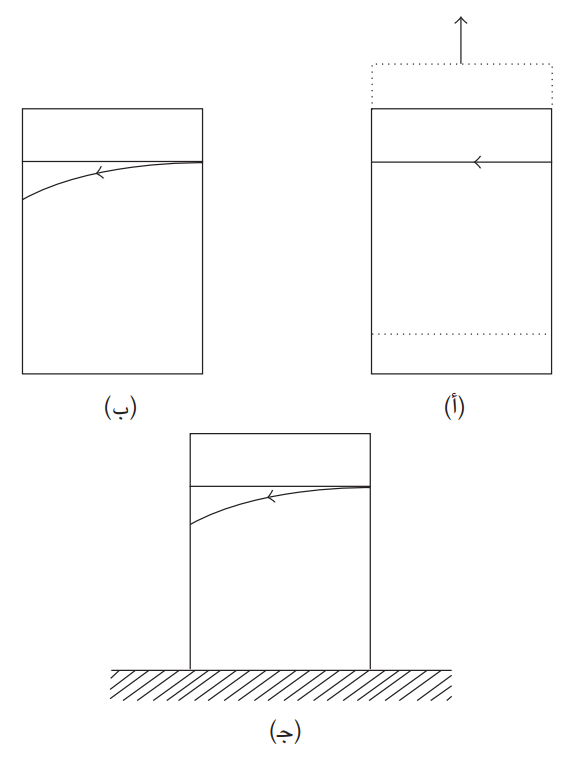
شكل 2: انحناء الضوء. في الحالة (أ) يتسارع المصعد إلى الأعلى. من منظور خارجي، يسير شعاع الليزر في خط مستقيم. في الحالة (ب)، من منظور داخلي يبدو أن شعاع الضوء ينحني إلى أسفل والتأثير عينه يحدث في المصعد الساكن الموجود داخل مجال جاذبية، وهو ما نراه في الحالة (ج).
فخلال الفترة الوجيزة التي استغرقها الشعاع في الانتقال من أحد الجانبين إلى الجانب الآخر ستكون حالة الحركة الخاصة بالمصعد قد تغيرت. فقد تسارع المصعد، وبذا صار يتحرك عند نهاية رحلة شعاع الضوء بسرعة أكبر مما كان الحال عند بداية هذه الرحلة. وهذا يعني أن النقطة التي سيرتطم بها شعاع الليزر في الحائط ستكون في موضع أكثر انخفاضًا بقليل من النقطة التي انطلق منها الشعاع على الجانب الآخر. فمن منظور الراصد الموجود داخل المصعد، تسبب التسارع في «إنحناء» شعاع الضوء إلى أسفل.
الآن تذكر حالة الزنبرك ومبدأ التكافؤ. حين لا يوجد تسارع، وإنما يوجد بدلًا منه مجال جاذبية يكون الموقف متشابها للغاية من منظور المصعد. تدبر الآن حالة مصعد موجود على سطح الأرض. يحدث لشعاع الضوء الأمر عينه تقريبًا الذي حدث في حالة المصعد المتسارع؛ إذ ينحني الضوء إلى أسفل. ومن هذا نخلص إلى أن الجاذبية تحني الضوء. وإذا لم تكن مسارات الضوء مستقيمة، بل منحنية، فهذا يعني أن المكان ليس منبسطا بل منحنيًا.
من أسباب صعوبة استيعاب عقولنا لفكرة المكان المنحني أننا لا نلحظ هذا الأمر في حياتنا اليومية. وهذا يرجع إلى أن الجاذبية تكون ضعيفة في الظروف الشائعة المعتادة. وحتى على نطاق المجموعة الشمسية، تكون الجاذبية ضعيفة لدرجة أن تأثير الانحناء الذي تتسبب فيه لا يُذكر، وينتقل الضوء في خطوط مقاربة للغاية للخطوط المستقيمة لدرجة أننا لا نلحظ الفارق. تُعَدُّ قوانين نيوتن بمنزلة تقريبات مفيدة للغاية لما يحدث، إلا أن هناك حالات علينا أن نُعِدَّ أنفسنا فيها للتعامل مع الجاذبية القوية.
 الاكثر قراءة في النظرية النسبية العامة
الاكثر قراءة في النظرية النسبية العامة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


