المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | اقتران زوجي Even Function |
 15219
 02:01 صباحاً
التاريخ: 29-10-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 43-44|
أقرأ أيضاً
التاريخ: 3-11-2015
1482
التاريخ: 27-11-2015
3187
التاريخ: 28-10-2015
5047
التاريخ: 15-11-2015
1309
|
هو الاقتران الذي تتطبق عليه القاعدة التالية :
ق(- س) = ق (س) لكل س∊ح كعدد حقيقي وهذا معناه ان قاعدة الاقتران ق(س) لا تتغير بوضع –س بدلاً من س في القاعدة المذكورة أعلاه .
وأما التفسير الهندسي لذلك فهو كما في الشكل .
اي ان منحنى الاقتران الزوجي متماثل حول محور الصادات والأمثلة عديدة منها :
ق(س) = | س |
حيث ق ( -س ) = | - س | = | س | = ق (س)
وكذلك ق (س) = س2
حيث ق ( - س)2 = س2 = ق(س)
ثم ق (س) = جتا س
حيث ق ( - س) = جتا – س = جتا س = ق(س)
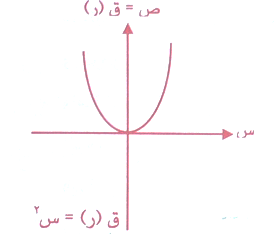
نلاحظ ان المنحنيات للاقترانات متماثلة حول محو الصادات .
|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تستعدّ لتكريم عددٍ من الطالبات المرتديات للعباءة الزينبية في جامعات كركوك
|
|
|
