Next, we may test what happens when we have two sources side by side several wavelengths apart (Fig. 28–3). The law is that the two sources should add their effects at point 1 when both of the sources are connected to the same generator and are both moving up and down the same way, so that the total electric field is the sum of the two and is twice as strong as it was before.

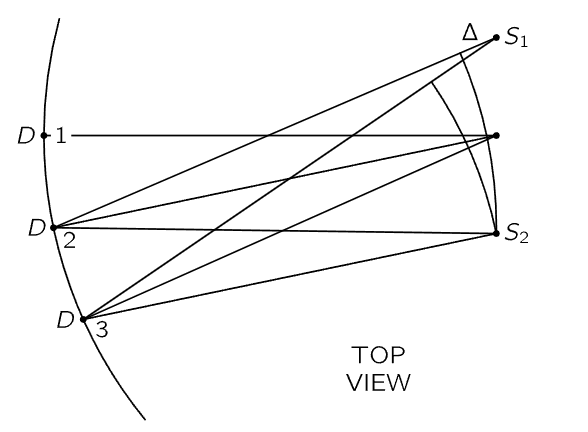
Fig. 28–3. Illustration of interference of sources.

Now comes an interesting possibility. Suppose we make the charges in S₁ and S₂ both accelerate up and down, but delay the timing of S₂ so that they are 180^∘ out of phase. Then the field produced by S₁ will be in one direction and the field produced by S₂ will be in the opposite direction at any instant, and therefore we should get no effect at point 1. The phase of oscillation is neatly adjustable by means of a pipe which is carrying the signal to S₂. By changing the length of this pipe, we change the time it takes the signal to arrive at S₂ and thus we change the phase of that oscillation. By adjusting this length, we can indeed find a place where there is no more signal left, in spite of the fact that both S₁ and S₂ are moving! The fact that they are both moving can be checked, because if we cut one out, we can see the motion of the other. So the two of them together can produce zero if everything is adjusted correctly.

Now, it is very interesting to show that the addition of the two fields is in fact a vector addition. We have just checked it for up and down motion, but let us check two nonparallel directions. First, we restore S₁ and S₂ to the same phase; that is, they are again moving together. But now we turn S₁ through 90^∘, as shown in Fig. 28–4. Now we should have at point 1 the sum of two effects, one of which is vertical and the other horizontal. The electric field is the vector sum of these two in-phase signals—they are both strong at the same time and go through zero together; the total field should be a signal R at 45^∘. If we turn D to get the maximum noise, it should be at about 45^∘, and not vertical. And if we turn it at right angles to that direction, we should get zero, which is easy to measure. Indeed, we observe just such behavior!

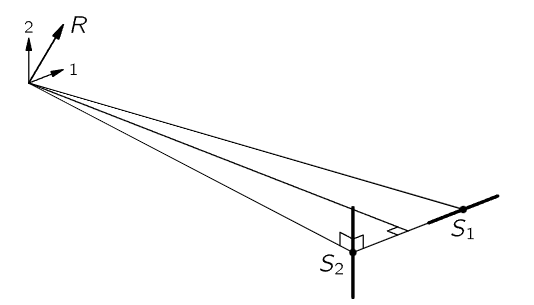
Fig. 28–4. Illustration of the vector character of the combination of sources.

Now, how about the retardation? How can we demonstrate that the signal is retarded? We could, with a great deal of equipment, measure the time at which it arrives, but there is another, very simple way. Referring again to Fig. 28–3, suppose that S₁ and S₂ are in phase. They are both shaking together, and they produce equal electric fields at point 1. But suppose we go to a certain place 2 which is closer to S₂ and farther from S₁. Then, in accordance with the principle that the acceleration should be retarded by an amount equal to r/c, if the retardations are not equal, the signals are no longer in phase. Thus, it should be possible to find a position at which the distances of D from S₁ and S₂ differ by some amount Δ, in such a manner that there is no net signal. That is, the distance Δ is to be the distance light goes in one-half an oscillation of the generator. We may go still further, and find a point where the difference is greater by a whole cycle; that is to say, the signal from the first antenna reaches point 3 with a delay in time that is greater than that of the second antenna by just the length of time it takes for the electric current to oscillate once, and therefore the two electric fields produced at 3 are in phase again. At point 3 the signal is strong again.

This completes our discussion of the experimental verification of some of the important features of Eq. (28.6). Of course, we have not really checked the 1/r variation of the electric field strength, or the fact that there is also a magnetic field that goes along with the electric field.