


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 29-12-2016
التاريخ: 2024-09-12
التاريخ: 10-3-2021
التاريخ: 22-11-2020
|
قوانين نيوتن هي القوانين الوحيدة في الميكانيكا الكلاسيكية وجميع «القوانين» أو المبادئ العامة الأخرى مستنتجة من قوانين نيوتن والفيزيائي يهتم على وجه الخصوص بالتعبيرات المتعلقة بسلوك أنظمة لا تعتمد على الطبيعة التفصيلية للقوة المعنية. وأفضل مثال معروف لمثل هذه التعبيرات هو مبدأ حفظ كمية التحرك:
إذا لم يتعرّض نظام ما لأي قوة خارجية، فإن كمية التحرك الكلية للنظام تبقى ثابتة في الزمن المحدد.
لفهم هذا النص، علينا بالطبع أن نعرف أولاً «كمية التحرك». إذا كان لدينا جسيم ما كتلته m وسرعته  ، فإن كمية تحرُّكه (يُرمز لها عادةً بالمتجه
، فإن كمية تحرُّكه (يُرمز لها عادةً بالمتجه  ) تُعرَّف بالمعادلة:
) تُعرَّف بالمعادلة:

وتعرف كمية تحرك نظام ما من الجسيمات بحاصل جمع كميات تحرك الجسيمات المفردة:

أثبتنا في الفصل الثالث (معادلة (10–3)) أنه لأي نظام:


حيث 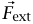 القوة الكلية الخارجية المؤثرة على النظام.
القوة الكلية الخارجية المؤثرة على النظام.
لاستنتاج المعادلة (3–4) نجمع معادلات القوة لجميع جسيمات النظام؛ تتلاشى القوى الداخلية أزواجًا أزواجًا كنتيجة لقانون نيوتن الثالث.
إذا كان 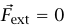 ، يكون لدينا المعادلة:
، يكون لدينا المعادلة:
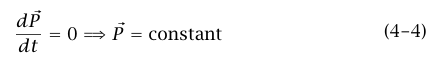
التي تسمى مبدأ حفظ كمية التحرك.
مثال 4–1 (تحليل تصادم تلتصق فيه الأجسام معًا). جسم كتلته 1kg وجسم كتلته 2kg يتصادمان على سطح أفقي أملس. قبل التصادم، كانت سرعة الجسم الأول 3 m/s في اتجاه شمال الشرق (أي 45o شرق الشمال) التصق الجسمان معًا، فتكون منهما كتلته 3kg. أوجد مقدار واتجاه سرعة الجسم الذي كتلته 3kg.
نختار اتجاه المحاور بحيث يشير المحور x إلى الشرق، والمحور y إلى الشمال، ويكون المحور z عموديًا على السطح. نعرف هذا النظام بأنه نظام الجسمين. وبما أن السطح أملس فلا توجد قوة خارجية في الاتجاه x أو الاتجاه y (لاحظ أنه يوجد قوى داخلية في النظام لأن الجسمين يؤثران أحدهما على الآخر أثناء وقت التصادم). تؤثّر قوة الجاذبية بشدة في الاتجاه z على كل جسم، لكن القوة العمودية التي يؤثر بها السطح تساوي قوة الجاذبية في المقدار وتُضادها في الاتجاه؛ وبناءً على ذلك لا يوجد صافي قوة خارجية على النظام، ونستطيع تطبيق مبدأ حفظ كمية التحرك الذي ينص على أن:


حيث vi مقدار متجه السرعة  . هذا لا ينتج من المعادلة (5–4)، وليس صحيحًا على وجه العموم. في المثال الحالي، المعادلة (6–4) ليست مهمة؛ فهي لا تنص إلا على أن 0 = 0. إذا سمينا متجه السرعة النهائية المجهولة
. هذا لا ينتج من المعادلة (5–4)، وليس صحيحًا على وجه العموم. في المثال الحالي، المعادلة (6–4) ليست مهمة؛ فهي لا تنص إلا على أن 0 = 0. إذا سمينا متجه السرعة النهائية المجهولة 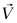 ومركبتيه Vx وVy، فإن المعادلتين (a6–4) و(b6–4) تعنيان أن:
ومركبتيه Vx وVy، فإن المعادلتين (a6–4) و(b6–4) تعنيان أن:

بهذا نجد أن Vx = 2.36 m/s وVy = 3.36 m/s. ويكون مقدار سرعة الجسم الذي كتلته 3kg هو  ويكون متجه السرعة V في اتجاه °55 شمال الشرق (°55 = tan–1 Vy/Vx).
ويكون متجه السرعة V في اتجاه °55 شمال الشرق (°55 = tan–1 Vy/Vx).
مثال 4–2 (تحليل تصادم ترتد فيه الأجسام بعيدًا). اعتبر نفس الجسمين المذكورين في المثال السابق متصادمين بنفس السرعتين الابتدائيتين، لكنهما لا يلتصقان معًا. بعد التصادم تكون سرعة الجسم الذي كتلته 2kg هي 4 m/s في اتجاه °30 شرق الشمال. سرعة الجسم الذي كتلته 1kg.
بتسمية السرعة المجهولة 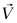 نجد من المعادلتين (a6–4) و (b6–4) أن:
نجد من المعادلتين (a6–4) و (b6–4) أن:

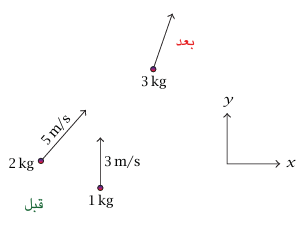
شكل 4–1: تصادم غير مرن.
لاحظ أنه عندما يلتصق الجسمان معًا (هذه الحالة تسمى التصادم غير المرن تمامًا)، فإن مبدأ حفظ كمية التحرك هو الذي يحدد منفردًا السرعة النهائية. وعندما لا يلتصق الجسمان معًا لا يكون مبدأ حفظ كمية التحرك هو الذي يحدد منفردًا متجه السرعة النهائية. إذا علم أحد متجهي السرعة النهائية، كما في المثال الحالي، فإن المتجه الآخر يحدد بمبدأ حفظ كمية التحرك. وبصورة أعم، يعيّن متجه ما في المستوى x–y بعددين (مثلا، مركبتا المتجه أو طول المتجه والزاوية التي يصنعها مع المحور x)؛ وبناءً عليه فإن أربعة أعداد تكون مطلوبة لتعيين متجهي السرعة النهائية. حفظ كمية التحرك x وكمية التحرك y بفرض ضرورة تحقيق شرطين (هما المعادلتان (a6–4) و(b6–4)) بواسطة هذه الأعداد الأربعة. وعلى ذلك ستتحدد الحالة النهائية إذا عين أي عددين من هذه الأعداد (مثلًا، اتجاها السرعتين النهائيتين). تعددية الحالات النهائية الممكنة تناظر حقيقة أن الجسمين لهما أشكال (والتلامس يمكن أن يحدث عند نقاط مختلفة على سطحيهما) ودرجات مختلفة من الصلابة (مثل كرتين من الصلب مقابل كرتي تنس قديمتين).
نعتبر الآن صاروخًا أُطلق رأسيًّا من الأرض، وفي لحظة ارتفاعه بسرعة 100 m/s انفجر إلى ثلاث شظايا متساوية الكتلة بعد الانفجار مباشرةً كانت سرعة إحدى الشظايا 50 m/s رأسيًّا إلى أسفل، وسرعة شظية أخرى 75 m/s في الاتجاه الأفقي. أوجد متجه سرعة الشظية الثالثة بعد الانفجار مباشرةً.
استطراد (مهم جدًا)
معظم الطلاب سوف يحلون هذه المسألة فورًا بمساواة كمية حركة الصاروخ قبل الانفجار مباشرةً مع حاصل كميات حركة الشظايا الثلاث بعد الانفجار مباشرةً. هذا الإجراء صحيح، ولكنه يستلزم بعض المناقشة لأن النظام لا يخلو من قوى خارجية؛ فقوة الجاذبية تؤثر على الصاروخ وتؤثر أيضًا على الشظايا. كيف نبرر إهمال تأثير الجاذبية؟ إذا أجرينا تكامل كلا طرفي المعادلة (3–4) بالنسبة إلى الزمن من t1 إلى t2، حيث t1 و t2اختياريان، نحصل على:

دعنا نختر t1 ليكون الزمن قبل الانفجار مباشرةً، و t2الزمن بعد الانفجار مباشرةً. في هذه المسألة  ؛ حيث M الكتلة الكلية للنظام، و
؛ حيث M الكتلة الكلية للنظام، و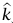 متجه وحدة رأسيا إلى أعلى. عندئذٍ يصبح الجانب الأيسر للمعادلة (10–4) هو
متجه وحدة رأسيا إلى أعلى. عندئذٍ يصبح الجانب الأيسر للمعادلة (10–4) هو 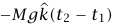 . يكون الانفجار «مثاليا» عندما يتطاير الصاروخ إلى أجزاء في زمن متناهي الصغر؛ أي 0 → t2 – t1 . في هذه الحالة يتلاشى الجانب الأيسر للمعادلة (10–4)، أو يكون مهملًا؛ وبهذا تكون كمية التحرك قبل الانفجار مباشرةً مساوية لكمية التحرك بعد الانفجار مباشرة.
. يكون الانفجار «مثاليا» عندما يتطاير الصاروخ إلى أجزاء في زمن متناهي الصغر؛ أي 0 → t2 – t1 . في هذه الحالة يتلاشى الجانب الأيسر للمعادلة (10–4)، أو يكون مهملًا؛ وبهذا تكون كمية التحرك قبل الانفجار مباشرةً مساوية لكمية التحرك بعد الانفجار مباشرة.
مثال 4–3 ( صاروخ منفجر). اعتبر المسألة المذكورة أعلاه للتو، والخاصة بصاروخ منفجر. إذا عرفنا 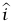 كمتجه وحدة مواز لسرعة الشظية المتحركة أفقيا، فإن حفظ كمية التحرك يستلزم أن يكون
كمتجه وحدة مواز لسرعة الشظية المتحركة أفقيا، فإن حفظ كمية التحرك يستلزم أن يكون
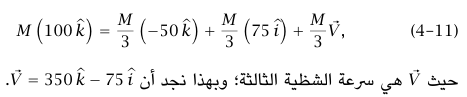
اقتراح ابتكر مسألة تعلم فيها الارتفاع الذي يحدث عنده الانفجار، وتعلم أيضًا مواضع النقاط التي تهبط عندها الشظايا (بالنسبة إلى النقطة التي تكون تحت الانفجار مباشرةً)، وأزمنة هبوطها (بالنسبة إلى زمن حدوث الانفجار). من هذه المعلومات تستطيع حساب سرعة الصاروخ قبل الانفجار مباشرةً. الحل سوف يشتمل على حفظ كمية التحرك بالإضافة إلى نتائج كينماتيكية من الفصل الأول).
مثال 4–4 الشد معًا على سطح لا احتكاكي طفلان أحدهما كتلته 30kg والآخر كتلته 45kg يقفان على بحيرة صغيرة متجمدة (بفرض أن الجليد أملس تمامًا). في البداية كانا ساكنين تمامًا وتفصلهما مسافة 30m، ويمسك كلُّ منهما بطرف حبل لا وزن له وطوله 30m، ثم بدأ الطفلان في شد الحبل إلى أن تصادما. أين سيحدث التصادم؟ (يجب أن توضّح طريقة الحل أن موقع نقطة التصادم لا يعتمد على تفاصيل كيفية شدّهما للحبل.)
تعرف نظامنا بأنه يتكون من طفلين بالإضافة إلى الحبل . وحيث إنه لا توجد قوة خارجية مؤثرة على النظام، يكون لدينا
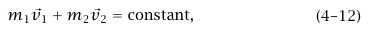
حيث  هي كتل وسرعات الطفلين. وبما أن
هي كتل وسرعات الطفلين. وبما أن  في البداية يساويان صفرا، فإن قيمة الثابت تساوي صفرًا؛ ومن ثُمَّ يكون:
في البداية يساويان صفرا، فإن قيمة الثابت تساوي صفرًا؛ ومن ثُمَّ يكون:

حيث 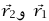 هما موضعا الطفلين بالنسبة إلى نقطة أصل ثابتة. إذا كان موضعا الطفلين الابتدائيان هما
هما موضعا الطفلين بالنسبة إلى نقطة أصل ثابتة. إذا كان موضعا الطفلين الابتدائيان هما 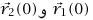 ، وموضع حدوث تصادمهما هو
، وموضع حدوث تصادمهما هو 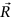 ، فإن:
، فإن:

من المناسب (ولكن ليس ضروريا) أن نأخذ نقطة الأصل عند موضع الطفل رقم 1 بحيث يكون 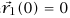 ، ويكون
، ويكون

مما يعني أنه إذا كانت المسافة الابتدائية الفاصلة بين الطفلين هي D، فإن التصادم يحدث على الخط بين الموضعين الابتدائيين عند نقطة تبعد مسافة D(m2/m1 + m2) عن الموضع الابتدائي للطفل رقم 1. في المثال الحالي، يحدث التصادم على بعد 18m من الموضع الابتدائي للطفل الأقل كتلة.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|