The semantics of scalar change

The assumptions outlined in the previous section (or something very much like them) are necessary to account for the semantics of the positive form, given a degree-based analysis of gradable adjectives.¹ They are not sufficient on their own, however, to explain the semantic properties of DAs in terms of the semantic properties of the adjectival parts of their meanings. To implement this hypothesis directly – essentially providing a scalar version of the Dowty/Abusch analysis – we would posit (1) as the meaning of a DA based on a gradable adjective g.

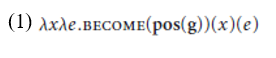
Here pos(g) is equivalent to the meaning of the positive form of a gradable adjective g. In the case of DAs based on adjectives whose positive forms make use of maximal standards (adjectives with upper closed scales), such as straight, dry, and dark, we almost get the right results. The DA straighten, for example, would have the denotation in (2).

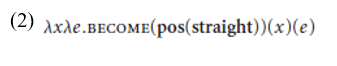
(2) is true of an individual x and an event e just in case pos(straight) is false of x at the beginning of e and true of x at the end of e. Since the measure function straight uses a scale with a maximum value, pos(straight) is true of x just in case it has maximal straightness, which in turn means that (2) holds of an event just in case x undergoes a change from non-maximal to maximal straightness. (2) fails to hold of subevents in which x ends up less than completely straight, and so is correctly predicted to be telic. However, this analysis will run into the same problems as Winter’s account: it predicts that straighten is never atelic, contrary to fact. This simple implementation fares even worse for DAs based on adjectives that do not have upper closed scales and maximum standards, however. Consider the case of widen, based on the open scale adjective wide, which should have the denotation in (3) according to (1).

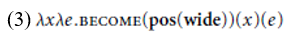
The problem is pos(wide) denotes the property of having a width that exceeds the standard of comparison for the context of utterance (whatever amount is enough to stand out relative to the measure function wide), so widen should have a meaning equivalent to become wide (which it doesn’t) and it should be telic (which it Isn’t). For the same reason, a DA like cool is predicted to have only a telic interpretation equivalent to become cool; (1) does not provide a means of deriving the atelic interpretation parallel to become cooler. One response to these problems would be to assume instead a version of Abusch’s “comparative” semantics as in (4).

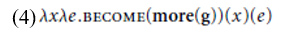
Strictly speaking, more in (4) cannot encode exactly the same meaning as the morpheme involved in comparative constructions, since the latter needs to combine with both an adjective and a standard of comparison (provided by the than-constituent in English) in order to derive a property of individuals. Instead, the more in (4) should really be thought of as shorthand for something that leaves us with a property that is true of an object x and an event e just in case x ends up being “more g at the end of e than it was at the beginning;” this is essentially the analysis of DAs proposed in Hay et al. (1999) and Winter (2006) (minus the culmination stipulation in the latter). (4) correctly captures the atelic interpretations of widen and cool, but fails to adequately account for the telic interpretation of the latter or to adequately explain why DAs like straighten and darken have default telic interpretations.

 It appears, then, that basing the semantics of DAs on a degree semantics of gradable adjectives fares no better than the Dowty/Abusch analysis. If we assume that DAs have only “positive” meanings like (1), we fail to account for atelic interpretations of widen, cool, straighten, and so forth. If we assume that DAs have only “comparative” meanings like (4) (essentially the position taken in e.g. Hay et al. 1999), we fail to derive the telic interpretations of straighten, darken, etc. Finally, if we assume that DAs are ambiguous between (1) and (4), the fact that widen, etc. do not have both atelic and telic interpretations (absent a measure phrase) becomes mysterious.

As a solution to this apparent paradox, we present a kind of synthesis of the “positive” and “comparative” analyses, which differs from both the Dowty/Abusch approach and the analyses of Hay et al. (1999), Kearns (2007), and Winter (2006) in the following crucial respect: instead of treating the adjectival part of the meaning of a DA as identical to the meaning of the adjectival base (a vague property for Abusch and Dowty; a measure function or the equivalent for Hay et al., Kearns, and Winter), we propose that the adjectival core of a DA is a special kind of derived measure function that measures the degree to which an object changes along a scalar dimension as the result of participating in an event.

Our analysis builds on a non-standard semantics of comparatives discussed in Kennedy and McNally (2005) (see also Faller 2000; Neeleman et al. 2004; Rotstein and Winter 2004 and Svenonius and Kennedy 2006; see Schwarzschild 2005 for a similar idea).² Noting that comparatives and deverbal adjectives with lower closed scales accept the same kinds of degree morphemes (e.g., both can be modified by much, as in much taller and much appreciated, which is indicative of a lower closed scale), Kennedy andMcNally propose that comparatives should be analyzed as derived measure functions, which are just like the functions expressed by the base adjective except that they use scales whose minimum values are determined by the denotation of the than-constituent – the “comparative standard.” Generalizing this idea, we can define for any measure function m a corresponding difference function Md ↑ that is just like m except that the degrees it returns for objects in its domain represent the difference between the object’s projection on the scale and an arbitrary degree d (the comparative standard): a positive value when there is a positive difference, and zero otherwise. This idea is made explicit in (5).

In the case of comparatives, the hypothesis is that the comparative morphology turns a basic measure function into a difference function with a scale whose minimal element – the “derived zero” – corresponds to the degree introduced by the comparative standard. So if wide denotes the measure function wide, wider than the carpet denotes the difference function widewide(c)↑, which returns values that represent the degree to which an object’s width exceeds that of the carpet (represented here as wide(c), which suppresses the temporal argument for perspicuity): positive values if the argument’s width is greater than that of the carpet, and zero (relative to the derived scale) otherwise.³ A consequence of this analysis is that like morphologically bare adjectives, comparative adjectives are of type _e, d_ and so need to combine with pos to derive a property of individuals. The denotation of the bracketed comparative predicate in (6a) is (6b), which is an abbreviation for the property in (6c) (which spells out the result of composition with pos).

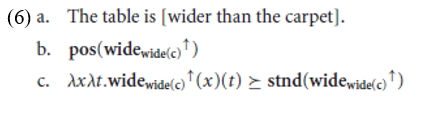
Given the semantics of the positive form discussed in the previous section, in particular the meaning contributed by stnd, (6c) is a property that is true of an individual if it stands out relative to the kind of measurement expressed by the difference function widewide(c)↑. Crucially, for any measure function m, a difference function md↑ based on m always uses a lower closed scale: one whose minimal element is d. Since measure functions with lower closed scales are systematically associated with minimum standards when they combine with pos, the result is that (6b) denotes a property that is true of an object x if the degree we get by applying the difference function to x is non-zero relative to the scale of the difference function, that is, is greater than wide(c). In other words, wider than the carpet is true of an object just in case its width exceeds the width of the carpet, which is exactly what we want.

Returning now to the semantics of DAs, we propose that the adjectival core of a degree achievement is a special kind of difference function: one that measures the amount that an object changes along a scalar dimension as a result of participating in an event. We make this idea explicit in (7), which defines for any measure function m from objects and times to degrees on a scale S a new measure of change function m_. (Here init and fin return the initial and final temporal intervals of an event.)

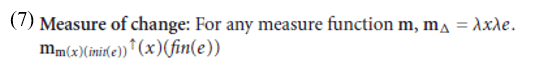
In prose, a measure of change function m_ takes an object x and an event e and returns the degree that represents the amount that x changes in the property measured by m as a result of participating in e. It does this by mapping its individual argument x onto a derived scale whose minimal element is the degree to which x measures m at the initiation of e. The output is a degree that represents the positive difference between the degree to which x measures m at the beginning of e and the degree to which it measures m at the end of e; if there is no positive difference, it returns zero.⁴

Like other measure functions, a measure of change must combine with some degree morphology (or undergo a type shift) in order to ensure that we ultimately end up with a property of events. We will consider overt instances of such morphology below; in order to complete the semantic analysis of Das we follow Pinon (2005) and posit a verbal positive form morpheme posv with the semantic properties stated in (8). (Here Dm_ represents the domain of measure of change functions – functions from individuals to functions from events to degrees.)

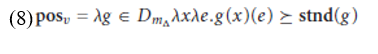
Combining posv with a measure of change function returns (9), which we claim represents the core (inchoative) meaning of a DA: a DA based on a measure of change function m_ is true of an object x and an event e just in the degree to which x changes as a result of participating in e exceeds the standard of comparison for m.

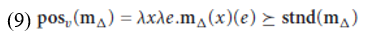
Before showing how this analysis derives the facts, we want to elaborate on two intuitions that underlie our proposal that Das are based on measure of change functions, rather than basic measure functions encoded by (non-comparative) gradable adjectives. The first is that any change necessarily entails a shift along some dimension, and that when that dimension is a scalar one, the change corresponds to a difference in degree. In this sense, a measure of change function generalizes (and directly encodes) the “transition” feature of Dowty’s become operator (where the shift from 0 to 1 represented by become is just the limiting case where the scale has no intermediate values). The second is that a fundamental part of what it means to make an adjective “verbal” is to introduce an event argument.

Thus the difference between a pure measure function or a comparative difference function (both adjectival roots) and a measure of change function (a verbal root) involves a difference in domain: the former are functions from objects and times to degrees; the latter is a function from objects and events to degrees. In the next section, we will show that this analysis both captures the truth conditions of DAs and accounts for their observed patterns of telicity in terms of the scalar properties of the measure of change function.

1 This is true regardless of whether we assume that such adjectives are of type _e, d_ or type_d, _e, t__,. The latter approach also requires a null positive morpheme, type shifting rule, or saturation principle to map a function of type _d, _e, t__ to a property of individuals.

2 The “standard” semantics for comparatives is one in which more than X is a quantifier over degrees that targets the degree argument of a gradable adjective; see Heim (2000) for a representative implementation.

3 We do not address here the question of how this degree is derived compositionally, though we see no obstacles to adapting any of a number of current proposals for the syntax and semantics of the comparative clause. Most analyses agree that the comparative clause denotes some sort of maximal degree (see e.g. von Stechow 1984; Rullmann 1995; Heim2000; Bhatt and Pancheva 2004), which is all that we need to build the derived scale.

4 Strictly speaking, (25) is not quite correct, because it does not ensure that what is measured is the degree to which x changes as a result of participating in e. That is because init and fin just return times, and not necessarily parts of e. This means that m_ can measure differences in an object relative to m over the time span of arbitrary events, rather than just events of x changing relative to m. We can fix this problem by assuming that init and fin return the minimal situations that correspond to the initial and final parts of e, and revising our semantics of measure functions accordingly, so they map individuals and situations to degrees, rather than individuals and times. We are grateful to Mark Gawron for pointing this out to us.