


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 30-11-2020
التاريخ: 10-2-2016
التاريخ: 15-2-2016
التاريخ: 2024-02-10
|
قوة الجاذبية قوة محافظة
لكي نرفع جسماً رأسياً إلى أعلى بسرعة ثابتة المقدار فإننا نحتاج إلى قوة تساوي وزن الجسم mg ، ونتيجة لذلك سيكون الشغل المبذول في رفع الجسم رأسياً إلى أعلى مسافة قدرها h هو mgh. سوف نثبت الآن أو نفس هذه النتيجة تظل صحيحة حتى إذا لم يرفع الجسم إلى أعلى في شكل رأسي .
لنفرض أننا نريد رفع الدلو المبين بالشكل ( 1أ) من الأرضية إلى سطح المنضدة. ما مقدار الشغل اللازم بذله لتحقيق ذلك؟ دعنا نرفع الجسم على المسار الممثل بالخط الواصل بين A و B بحيث تكون قوة الرفع متجهة رأسياً إلى أعلى خلال الحركة كلها.
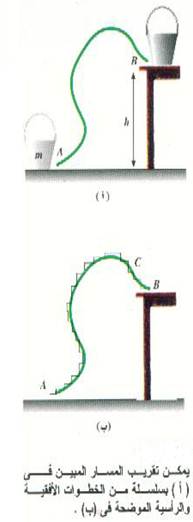
الشكل (1)
احساب الشغل المبذول في رفع الدلو من A إلى B يمكننا تقريب المسار الفعلي إلى مسار مدرج كالمبين بالجزء (ب) من الشكل. بجعل أطوال الدرجات صغيرة جداً سيصبح المسار المدرج مماثلاً للمسار الأملس المبين بالشكل ( 1ب). ونظراً لأن قوة الرفع رأسية قوة الرفع تبذل شغلاً في الحركات الرأسية فقط . يلاحم الأفقية على المسار المدرج ، أي أن قوة الرفع تبذل شغلاً في الحركات الرأسية فقط. يلاحظ كذلك أن الشغل المبذول يكون موجباً عند ارتفاع الدلو ، ولكنه يكون سالباً إذا انخفض الجسم في أي نقطة على مساره ( بالقرب من C مثلاً). معنى ذلك أن الشغل المبذول في الحركات الرأسية إلى أسفل يلاشي الشغل المبذول في الحركات الرأسية المكافئة إلى أعلى. ويستنتج من ذلك أن الشغل المبذول يعتمد فقط على صافي تأثير جميع الحركات الرأسية. الخلاصة إذن أن انتقال الدلو وكتلته m ، من A إلى B معناه أن الدلو قد ارتفع إلى أعلى مسافة قدرها h، ومن ثم فإن الشكل المبذول في هذه العملية يساوي mgh وهو نفس الشغل المبذول في رفع الجسم من A مسافة رأسية قدرها h ثم تحريكه جانباً إلى النقطة B. وحيث ان المسار الموضح من A إلى B اختياري تماماً في الواقع يمكننا استنتاج أنه:
إذا كانت النقطة A تقع على بعد قدره h تحت النقطة B فإن الشغل المبذول ضد قوة الجاذبية لرفع كتلة قدرها m من A الى B مساوي mgh.
هذه النتيجة صحيحة لأي مسار بين A و B طالما لم تتغير g نتيجة للانتقال من A إلى B . ومن الطبيعي أنه غذا خفضت الكتلة من B إلى A فإن الشعل المبذول ضد الجاذبية سيكون – mgh.
قوة الجاذبية مثال لما يسمى بالقوة المحافظة.
يقال أن القوة محافظة إذا كان الشغل المبذول في تحريك جسم من نقطة A إلى اخرى B ضد هذه القوة لا يعتمد على مسار الحركة.
وسوف نرى ان القوى الكهروستاتيكية والنووية هي قوى محافظة. هذا صحيح أيضاً بالنسبة للقوى المرنة مثل القوى المتولدة في زنبرك ممتد أو منضغط. أما قوي الاحتكاك ، من ناحية أخرى ، فهي قوى غير محافظة. هذا ما يمكنك التحقق منه بسهوة بأن تزلق كتابك من نقطة إلى أخرى على منضدة حيث سيتضح لك انه ستضطر إلى بذل شغل أكبر عندما تزلقه في مسار معقد طويل عنه في حالة اتباعك لمسار على هيئة خط مستقيم. بناء على ذلك يقال لقوة بأنها قوة غير محافظة إذا كان الشغل المبذول بواسطة القوة يعتمد على مسار الحركة بين نقطتين معينتين ، كما في حالة الاحتكاك.
الطريقة المكافئة الأخرى للتمييز بين القوى المحافظة وغير المحافظة هي أنه من الممكن تعريف طاقة جهد مرتبطة بالقوة المحافظة ، بينما هذا غير ممكن في حالة القوى غير المحافظة لأنها تعتمد على المسار وليس على مجرد الموضع فقط.
ولكي نرى لماذا توصف بعض القوى بأنها محافظة سوف تعرف الطاقة الميكانيكية (ME) للنظام بنها مجموع طاقتي الحركة والجهد لهذا النظام:
ME = KE + PE
حيث يمكن ان يتضمن الحد الممثل لطاقة الجهد في هذا التعريف اكثر من نوع واحد من طاقة الجهد عندما يؤثر على النظام من قوة محافظة واحدة. وهنا نجد أن الطاقة الميكانيكية للنظام تظل محفظة ، أو ثابتة ، أثناء حركة انظام تحت تأثير القوة المحافظة فقط. ومن ثم يمكننا تلخيص خاصية في غاية الأهمية للقوى المحافظة على الصور الآتية:
القوة المحافظة هي تلك القوة التي تحفظ الطاقة الميكانيكية للنظام.
هذه الصيغة هي إحدى صور صيغة اكثر عمومية تسمى بقاء الطاقة. هذا وتعتمد قوانين البقاء من اهم القوانين في الفيزياء عموماً إذا أنها تخبرنا أي الكميات الفيزيائية تظل ثابتة عند حدوث تغيرات في النظام الفيزيائي.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|