


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-2-2016
Date: 22-2-2016
Date: 28-2-2016
|
The number 1 is important but what about 11? It is interesting too and so is 11 × 11 = 121, 11 × 11 × 11 = 1331 and 11 × 11 × 11 × 11 = 14,641. Setting these out we get

These are the first lines of Pascal’s triangle. But where do we find it?
Throwing in 11° = 1 for good measure, the first thing to do is forget the commas, and then introduce spaces between the numbers. So 14,641 becomes 1 4 6 4 1.

Pascal’s triangle is famous in mathematics for its symmetry and hidden relationships. In 1653 Blaise Pascal thought so and remarked that he could not possibly cover them all in one paper. The many connections of Pascal’s triangle with other branches of mathematics have made it into a venerable mathematical object, but its origins can be traced back much further than this. In fact Pascal didn’t invent the triangle named after him – it was known to Chinese scholars of the 13th century.
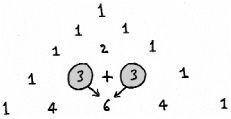
The Pascal pattern is generated from the top. Start with a 1 and place two 1s on either side of it in the next row down. To construct further rows we continue to place 1s on the ends of each row while the internal numbers are obtained by the sum of the two numbers immediately above. To obtain 6 in the fifth row for example, we add 3 + 3 from the row above. The English mathematician G.H. Hardy said ‘a mathematician, like a painter or a poet, is a maker of patterns’ and Pascal’s triangle has patterns in spades.
Links with algebra
Pascal’s triangle is founded on real mathematics. If we work out (1 + x) × (1 + x) × (1 + x) = (1 + x)3, for example, we get 1 + 3x + 3x2 + x3. Look closely and you’ll see the numbers in front of the symbols in this expression match the numbers in the corresponding row of Pascal’s triangle. The scheme followed is:

If we add up the numbers in any row of Pascal’s triangle we always obtain a power of 2. For example in the fifth row down 1 + 4 + 6 + 4 + 1 = 16 = 24. This can be obtained from the left-hand column above if we use x = 1.
Almost diagonals in Pascal’s triangle
Properties
The first and most obvious property of Pascal’s triangle is its symmetry. If we draw a vertical line down through the middle, the triangle has ‘mirror symmetry’ – it is the same to the left of the vertical line as to the right of it. This allows us to talk about plain ‘diagonals’, because a northeast diagonal will be the same as a northwest diagonal. Under the diagonal made up of 1s we have the diagonal made up of the counting numbers 1, 2, 3, 4, 5, 6, . . . Under that there are the triangular numbers, 1, 3, 6, 10, 15, 21, . . . (the numbers which can be made up of dots in the form of triangles). In the diagonal under that we have the tetrahedral numbers, 1, 4, 10, 20, 35, 56, . . . These numbers correspond to tetrahedra (‘three-dimensional triangles’, or, if you like, the number of cannon balls which can be placed on triangular bases of increasing sizes). And what about the ‘almost diagonals’?
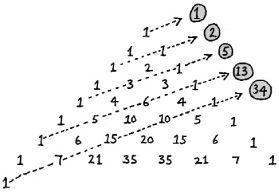
If we add up the numbers in lines across the triangle (which are not rows or true diagonals), we get the sequence 1, 2, 5, 13, 34, . . . Each number is three times the previous one with the one before that subtracted. For example 34 = 3 × 13 – 5. Based on this, the next number in the sequence will be 3 × 34 – 13 = 89. We have missed out the alternate ‘almost diagonals’, starting with 1, 1 + 2 = 3, but these will give us the sequence 1, 3, 8, 21, 55, . . . and these are generated by the same ‘3 times minus 1’ rule. We can therefore generate the next number in the sequence, as 3 × 55 – 21 = 144. But there’s more. If we interleave these two sequences of ‘almost diagonals’ we get the Fibonacci numbers:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .

Even and odd numbers in Pascal’s triangle
Pascal combinations
The Pascal numbers answer some counting problems. Think about 7 people in a room. Let’s call them Alison, Catherine, Emma, Gary, John, Matthew and Thomas. How many ways are there of choosing different groupings of 3 of them? One way would be A, C, E; another would be A, C,T. Mathematicians find it useful to write C(n,r) to stand for the number in the nth row, in the rth position (counting from r = 0) of Pascal’s triangle. The answer to our question is C(7,3). The number in the 7th row of the triangle, in the 3rd position, is 35. If we choose one group of 3 we have automatically selected an ‘unchosen’ group of 4 people. This accounts for the fact that C(7,4) = 35 too. In general, C(n,r) = C(n, n – r) which follows from the mirror symmetry of Pascal’s triangle.

The Serpiński gasket
0s and 1s
In Pascal’s triangle, we see that the inner numbers form a pattern depending on whether they are even or odd. If we substitute 1 for the odd numbers and 0 for the even numbers we get a representation which is the same pattern as the remarkable fractal known as the Sierpinski gasket.
Adding signs
We can write down the Pascal triangle that corresponds to the powers of (−1 + x), namely (−1 + x)n.

Adding signs
In this case the triangle is not completely symmetric about the vertical line, and instead of the rows adding to powers of 2, they add up to zero. However it is the diagonals which are interesting here. The southwestern diagonal 1, −1, 1, −1, 1, −1, 1, −1, . . . are the coefficients of the expansion while the terms in the next diagonal along are the coefficients of the expansion
(1 + x)−1 = 1 − x + x2 − x3 + x4 − x5 + x6 − x7 + . . .

The Leibniz harmonic triangle
(1 + x)−2 = 1 – 2x + 3x2 – 4x3 + 5x4 – 6x5 + 7x6 – 8x7 + . . .
The Leibniz harmonic triangle
The German polymath Gottfried Leibniz discovered a remarkable set of numbers in the form of a triangle. The Leibniz numbers have a symmetry relation about the vertical line. But unlike Pascal’s triangle, the number in one row is obtained by adding the two numbers below it. For example 1/30 + 1/20 = 1/12. To construct this triangle we can progress from the top and move from left to right by subtraction: we know 1/12 and 1/30 and so 1/12 − 1/30 = 1/20, the number next to 1/30. You might have spotted that the outside diagonal is the famous harmonic series

but the second diagonal is what is known as the Leibnizian series

which by some clever manipulation turns out to equal n/(n + 1). Just as we did before, we can write these Leibnizian numbers as B(n,r) to stand for the nth number in the rth row. They are related to the ordinary Pascal numbers C(n,r) by the formula:

In the words of the old song, ‘the knee bone’s connected to the thigh bone, and the thigh bone’s connected to the hip bone’. So it is with Pascal’s triangle and its intimate connections with so many parts of mathematics – modern geometry, combinatorics and algebra to name but three. More than this it is an exemplar of the mathematical trade – the constant search for pattern and harmony which reinforces our understanding of the subject itself.
the condensed idea
The number fountain




|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تستعدّ لتكريم عددٍ من الطالبات المرتديات للعباءة الزينبية في جامعات كركوك
|
|
|