


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
أقرأ أيضاً
التاريخ: 19-3-2016
التاريخ: 15-10-2015
التاريخ: 1-3-2016
التاريخ: 15-3-2016
|
يهدف هذا البند إلى استنتاج بعض الصفات الأساسية للتحويلات الخطية العامة.
مبرهنة (1-1):
لتكنW⟶T :V تحويلة خطية، فإن مجموعة جميع المتجهات في V التي صورة كل منها بواسطة T تساوي صفر تسمى نواة T وتكتب (kernel T) Ker T. اما مجموعة جميع المتجهات في W والتي هي عبارة عن صورة لعلى الأقل متجه واحد في V بواسطة T، تسمى مدى T، وتكتب (Image T) Im(T).
يمكن تعريف كل من Ker (T) و Im (T) جبرياً على النحو الآتي:
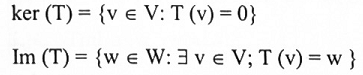
مثال(1) :
لتكن T:R3⟶R3 تطبيق إسقاطي والمعرف بالشكل:
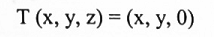
أوجد Ker T و Im T
الحل:
واضح ان النقاط على المحور z تكون صورتها بواسطة T هي المتجه الصفري 0 لذا فإن 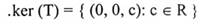 أما صورة T فتتكون من جميع النقاط في المستوى xy، أي،
أما صورة T فتتكون من جميع النقاط في المستوى xy، أي،
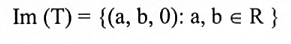
مثال(2):
لتكن W⟶T:V تطبيق خطي فإن Ker (T) فضاء جزئي في V و Im (T) فضاء جزئي في W.
الحل:
بما أن T(0) = 0 فإن 0∊ker T (أي أن Ker T غير خالية).
نفرض . ∊ker T u,v إذن T(v) = 0 و T(u) = 0. لذا فإن:

إذن Ker T فضاء جزئي في V.

وبنفس الطريقة شرط الضرب.
مثال(3):
لتكن T:R4⟶R3 تحويلة خطية معرفة بالشكل:

أوجد أساس وبعد صورة T.
الحل: نوجد صور المتجهات الطبيعية للفضاء R4.
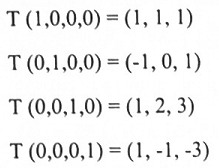
عليه فإن متجهات صور T تنشأ (T) Im (صورة T). بوضع هذه المتجهات بشكل صفوف وبموجب الشكل المدرج الصفي المختزل نحصل على: 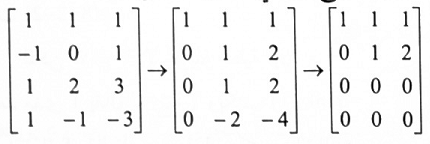
لذا فإن : {(1,1,1) , (0,1,2)} أساس Im (T).
عليه فإن بعد Im (T) هو 2.
مثال(4):
أوجد أساس وبعد Ker (T) للتحويلة الخطية في المثال 3.
الحل:
نفرض T(v) = 0 حيث v = (x,y,s,t)
أي:
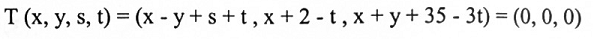
وبمقارنة مركبات المتجهات لطرفي المعادلة أعلاه نحصل على:
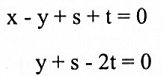
حيث t, s هي المتغيرات الحرة، لذا فإن بعد النواة هو 2.
وبإعطاء قيم لأعلى التعين لـ t, s كالآتي:
عندما s = -1 و 1= 0 نحصل على الحل: (2, 1,-1,0).
وعندما s = 0 و t = 1 نحصل على الحل: (1,2,0,1).
لذا فإن: {(2,1,-1,0) , (1,2,0,1)} هو أساس Ker (T)
لقد عرفنا في البند رتبة المصفوفة بأنه بعد فضاء أعمدتها وصفرية المصفوفة بأنها بعد فضائها الصفري. سنحاول الآن تعميم هذه التعاريف على التحويلات الخطية العامة.
تعريف (1-2):
لتكن W⟶T:V تحويلة خطية فإن:
1. بعد مدى T يقال له رتبة T ويكتب rank (T).
2. بعد نواة T يقال له صفرية T ويكتب null (T).
مبرهنة (1-2):
إذا كانت A مصفوفة سعتها m x n و TA:Rn⟶Rm مضروبة A فإن:
1. صفرية (TA) = صفرية (A).
2. رتبة (TA) = رتبة (A).
البرهان:
لما كانت A سعتها m x n و TA:Rn⟶Rm مضروبة A وبموجب المناقشات في الفصول السابقة فإن نواة TA هي فضاء A الصفري.
ومدى TA هو فضاء أعمدة A.
مثال(5):
لتكن T:R4⟶R4 مضروبة A. أوجد رتبة وصفرية TA
حيث:

الحل:
من المثال 8 في (رتبه المصفوفه) وجدنا أن رتبة A هي 3 وصفرية A هي 1. لهذا وبموجب مبرهنة (1-3) نحصل على
رتبة TA هي 3 وصفرية TA هي 1.
مبرهنة (1-4):
لتكن W⟶T:V تحويلة خطية من فضاء المتجهات الذي بعده n إلى فضاء المتجهات W فإن:
(1) .......................................... رتبة T + صفرية n = T
أو:
N =rank (T) + null (T)
أو:
بعد مدى T + بعد نواة n = T
مثال(6):
من الأمثلة 3 و 4 وجدنا أن بعد مدى T هو 2 وبعد نواة T هو 2 وبموجب مبرهنة (1-4) نجد أن:
رتبة T + صفرية 4 = 2+2 = T وهذه تساوي بعد منطلق T.
مثال(7):
من المثال(1) وجدنا ان بعد مدى T هو 1 وبعد نواتها هو 2 لذا فإن:
2+1 = 3 وهو عبارة عن بعد منطلق T.
أي أن:
رتبة T + صفرية T = رتبة منطلق T.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تحتفي بذكرى ولادة الإمام الجواد (عليه السلام) في مشاتل الكفيل
|
|
|