
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
PULSE POWER AND ENERGY
المؤلف:
Mark Csele
المصدر:
FUNDAMENTALS OF LIGHT SOURCES AND LASERS
الجزء والصفحة:
p198
20-3-2016
2626
PULSE POWER AND ENERGY
It becomes evident, then, that at the moment the switch is opened, the initial inversion (ΔNi) is many times larger than the threshold inversion (ΔNth), which a continuous laser cannot normally exceed. We begin a mathematical analysis of a Q-switched laser by considering the number of coherent photons inside the cavity (per unit volume) at any given time, denoted n. More specifically, we consider the rate at which the number of photons increases or decreases in the cavity as
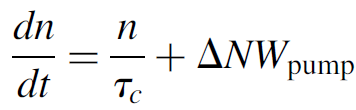 (1.1)
(1.1)
where τc is the lifetime of a photon in the cavity, ΔN is the population inversion at any given time t, and Wpump is the pumping probability. The left side of the equation (n/τc) represents the rate of photon loss in the cavity simply the number of photons divided by the lifetime of a photon and the right side of the equation represents the rate of photon gain simply the inversion times the pumping probability. We may now simplify the equation knowing that the pump rate can be expanded according to
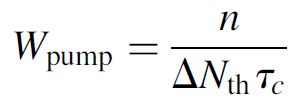 (1.2)
(1.2)
where ΔNth is the threshold population inversion. Equation (1.1) then simplifies to
 (1.3)
(1.3)
which expresses the rate of change of the number of photons in the cavity. Just before the switch is opened, ΔN/ΔNth assumes a large value and n is essentially zero.
To solve the problem, two equations are required. For the second we now revisit the rate equations for a laser to generate an expression for the rate of change ΔN. You will recall the development of rate equations for the ULL of two-, three-, and four-level atomic systems, but in a real laser, stimulated processes are also at work. In a three-level laser, for example, the rate equation for the ULL becomes
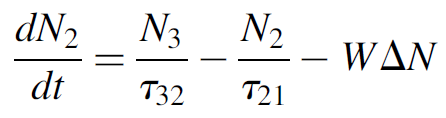 (1.4)
(1.4)
which is with added terms for stimulated processes where the first term represents input from the pump level; the second term, spontaneous decay. We may develop an exceedingly simply expression for dΔN/dt (the rate of change of the inversion) by making a few assumptions: namely, that the Q-switch pulse occurs so quickly that the effects of decay from the pump level (the first term) as well as the effects of spontaneous emission (the second term) are quite negligible during the time the actual pulse is generated. We also note that for a three level laser a loss of one atom from the ULL results in a gain of one atom in the LLL, so the total change in the difference (ΔN) is 2. The answer is then simply
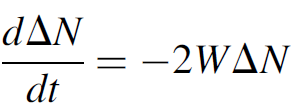 (1.5)
(1.5)
Further substitution for W using equation (1.2) yields
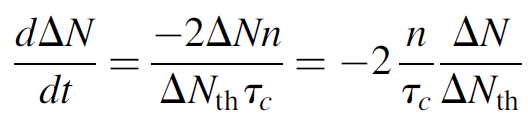 (1.6)
(1.6)
which allows us to simply divide equation (1.3) by equation (1.6) to form an expression for the change in the number of coherent photons with respect to the change in population inversion:
 (1.7)
(1.7)
This differential equation may be mathematically integrated to yield an answer in terms of the number of coherent photons:
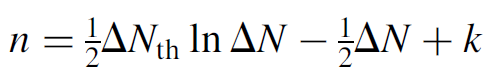 (1.8)
(1.8)
where k is a constant. To solve for the constant, we apply initial conditions in which there is no output (i.e., n = 0) just before the switch opens and the inversion is at its initial, peak value of ΔNinitial:
 (1.9)
(1.9)
so that equation (1.8) assumes the final form
 (1.10)
(1.10)
We have now solved equation (1.10) for the number of photons per unit volume in the cavity [the reader is reminded, though, that n is actually a function of time, so that, most properly, it should be written as n(t)]. We also presumably know the volume of the cavity and the energy of each photon (hv), so that the output power for the Q-switched pulse can be computed as
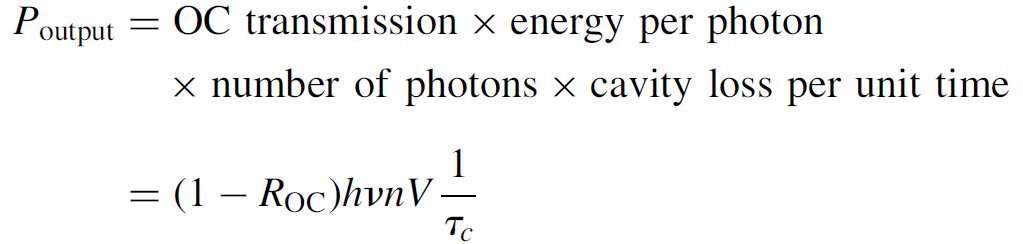 (1.11)
(1.11)
You will recall that τc represents the total distributed losses (of coherent photons) in the cavity. This expression, then, gives the instantaneous power of the pulse (in watts) at any time t. The total energy of the pulse can be determined by integrating the power over the entire time frame of the pulse:
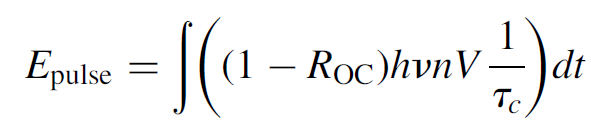 (1.12)
(1.12)
Since only n is a function of time, the calculus is straightforward, but the time dependence of ΔN must then be determined. The integration may be made easier by realizing that we may integrate over ΔN since we know that it starts at value ΔNinitial and ends at some terminal value ΔNfinal (for which we may, for many practical purposes, substitute ΔNthresold, especially if pumping is strong enough so that the laser continues to operate in CW mode after the switch is opened and the pulse is produced). The integral then becomes
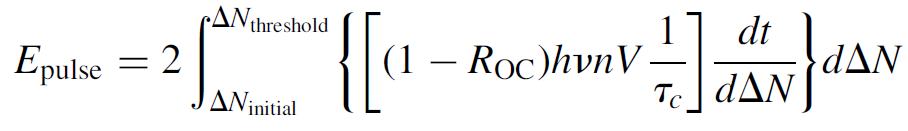 (1.13)
(1.13)
where the “2” in front corrects for the fact that the pulse is only half over when the threshold value is reached (assuming a symmetrical pulse). The term dt/dΔN can then be substituted for the inverse of equation (1.6) (also in terms of ΔN). Constant terms (such as ROC, hv, and threshold inversion ΔNth) are pulled out of the integral and several terms cancel, to yield a simple integral:
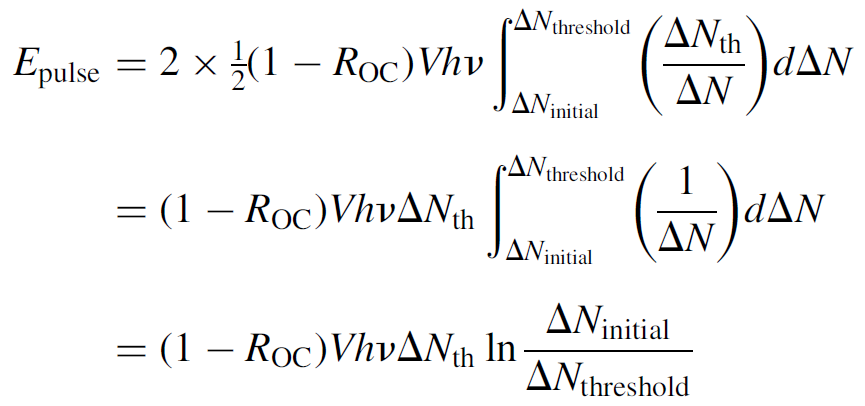 (1.14)
(1.14)
An exceedingly simple result! Bear in mind that assuming pulse termination at the threshold inversion and then multiplying by 2 is indeed a simplification of the problem, since real Q-switched pulses usually have a longer tail. The estimate provided here will yield an answer somewhat lower than the actual output, although results will vary according to the ratio of ΔNinitial /ΔNthreshold, but generally it is found to be within 20% of experimental results. Peak power is of particular interest for a Q-switched laser since this is the reason for using the technique in the first place. At peak power, the rate of change of the number of photons will be zero (i.e., at the top of the peak itself, where the curve is essentially horizontal). Setting dn/dt = 0 in equation (1.3), we find that the peak power occurs when ΔN = ΔNth [of course, we knew this already since we used it as a basis for the simplification in equation (1.13)]. By substituting this value into equation (1.10), we can obtain an exact expression for the number of coherent photons per unit volume at the peak of the pulse. Further simplification is possible if we assume that ΔNinitial is much, much larger than ΔNth (logical since this is required to produce giant pulses), so we can neglect many terms in the result to find that
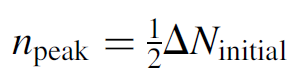 (1.15)
(1.15)
Substitution into equation (1.11) is straightforward and yields an answer of
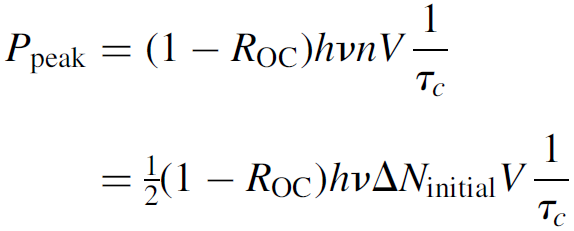 (1.16)
(1.16)
Using previous results, it is also possible to characterize the width of the pulse as
 (1.17)
(1.17)
Once again, this is an approximation. Exact solutions are possible, but these require a good deal of calculus.
 الاكثر قراءة في مواضيع عامة في علم البصريات
الاكثر قراءة في مواضيع عامة في علم البصريات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















