


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 3-9-2016
Date: 13-7-2016
Date: 11-8-2016
|
Mud from Tire
A car is stuck in the mud. In his efforts to move the car, the driver splashes mud from the rim of a tire of radius R spinning at a speed v, where v > gR Neglecting the resistance of the air, show that no mud can rise higher than a height R+ v2 /2g+ gR2/2v2 above the ground.
SOLUTION
Mud flying from different points on the tire will rise to different heights, depending on the initial height and angle of ejection. Introducing an angle α and the height h of the point of ejection O above the equator of the tire (see Figure 1.1), we can write using energy conservation
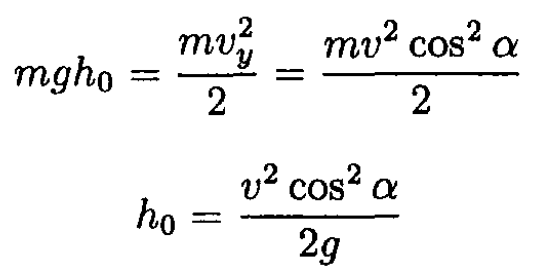
where h0 is the height to which the mud rises above O, and v = ωR is the speed of the rim of the wheel. The height H above the ground will be
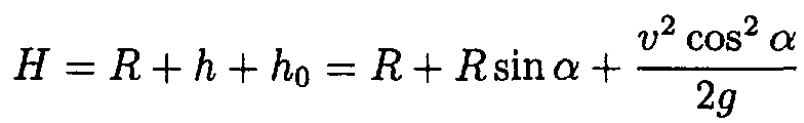
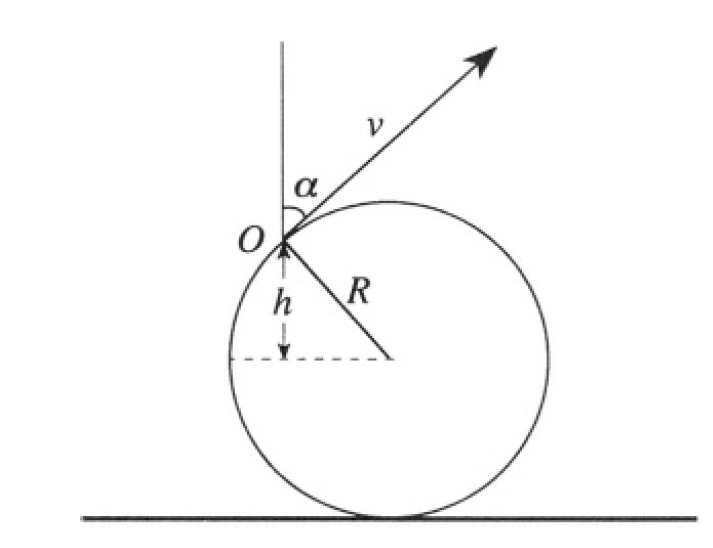
Figure 1.1
Now find the maximum height by setting the derivative of H with respect to α equal to 0:
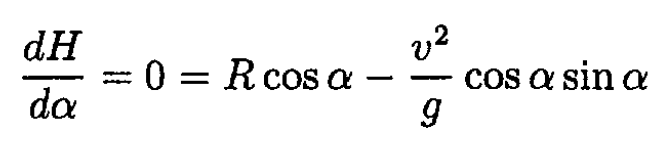
There are two solutions of this equation. First,
 (1)
(1)
This case yields a maximum only when v2 ≤ gR, and the highest point of the wheel is the maximum height. But here v2 > gR, so we will consider the other case:
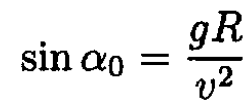 (2)
(2)
The height becomes
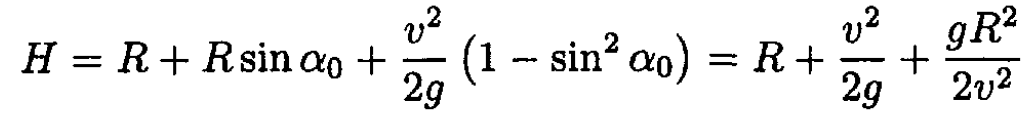
We can check that
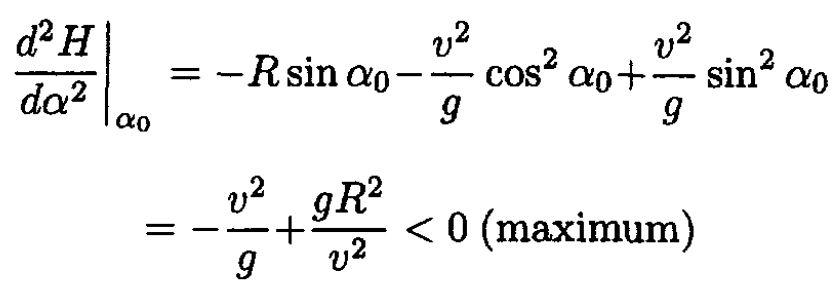



|
|
|
|
حقن الذهب في العين.. تقنية جديدة للحفاظ على البصر ؟!
|
|
|
|
|
|
|
"عراب الذكاء الاصطناعي" يثير القلق برؤيته حول سيطرة التكنولوجيا على البشرية ؟
|
|
|
|
|
|
|
المجمع العلمي يعقد اجتماعاً لمناقشة إطلاق مشروع الدورات القرآنيّة الصيفيّة
|
|
|