
آخر المواضيع المضافة


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 14-8-2016
Date: 19-8-2016
Date: 29-8-2016
|
Period as Function of Energy
A particle of mass m moves in a one-dimensional potential U(x) = A |x|n where A is a constant. Find the dependence of the period τ on the energy E in terms of n.
SOLUTION
Energy is conserved for a position dependent potential, so we may write E = (1/2) mẋ2 + A |x|n. The time for a particle to travel between two turning points of its motion τ1 and τ2 (where its kinetic energy is zero) is given by
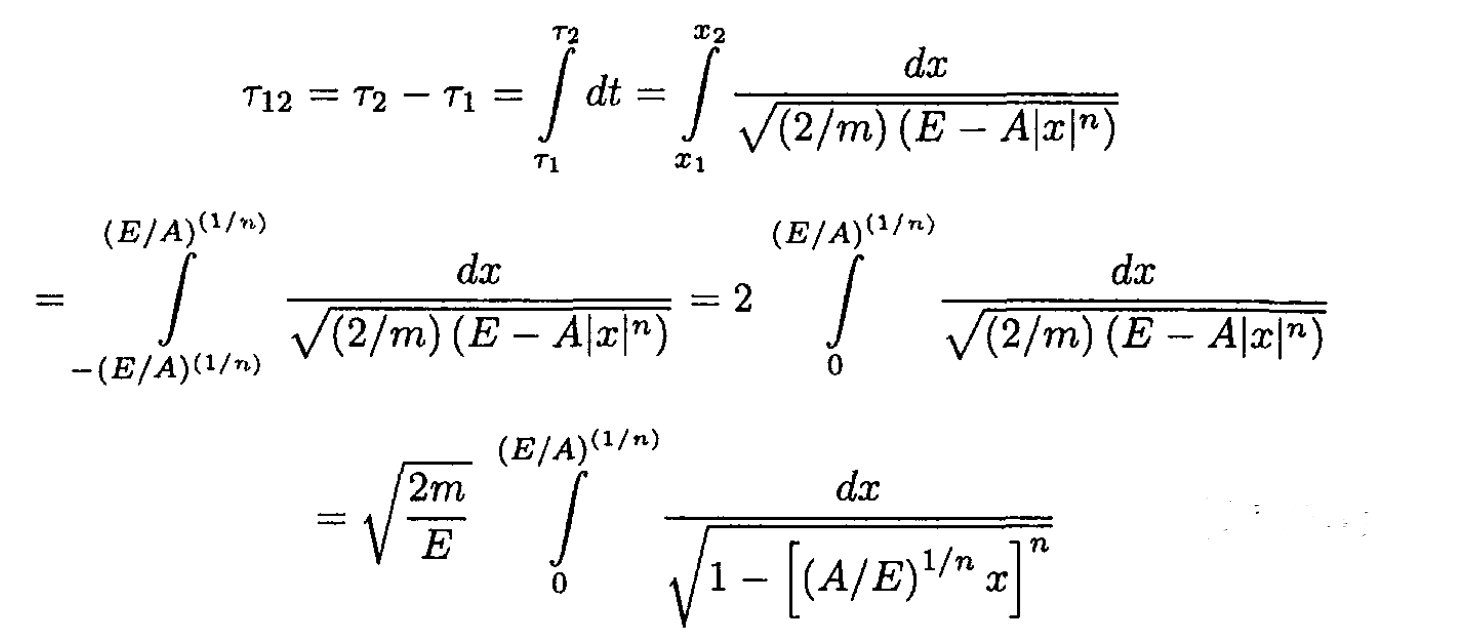 (1)
(1)
Let u = (A/E)1/n x. (1) then becomes
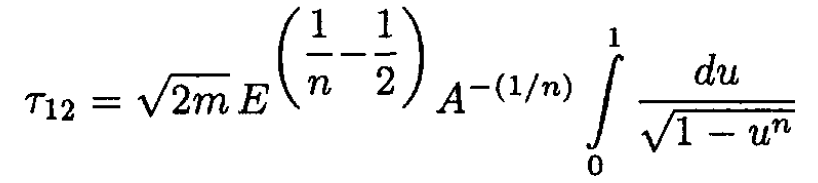 (2)
(2)
The period T is twice the time to go between points 1 and 2, T = 2τ12. So for the energy dependence of the period, we have
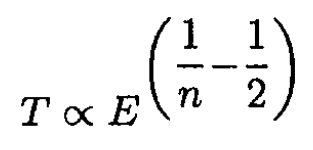 (3)
(3)
For a harmonic oscillator n = 2, and 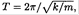 independent of E, as (3) confirms
independent of E, as (3) confirms



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|