

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Degrees
المؤلف:
Jean-Claude Fournier
المصدر:
Graph Theory and Applications
الجزء والصفحة:
33-35
2-8-2016
2109
The degree of a vertex x in a graph G is the number of edges in G incident to x, that is edges with x as an end vertex, loops being counted twice. This integer is denoted by d(x)or dG(x). For example, for the graph in Figure 1.1:d(x)=3, d(y)=4, d(z)=3.
Avertexis isolated if its degree equals zero. Dealing with degrees is anopportunity to state the following proposition.
Another definition
The degree of vertex v in a graph G, written dG(v) or d(v), IS the number of edges incident to v, except that each loop at v counts twice.
The maximum degree is∆ (G), the minimum degree is δ (G), and G is regular ifδ (G) = ∆(G). It is k-regular if the common degree is k. The neigh-
borhood of v, written NG(v) or N(v), is the set of vertices adjacent to v.
Proposition 1.1.
In any graph G, we have:
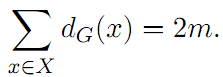
Proof. When adding up the vertex degrees of G, each edge is counted twice ,once for each end (this is particularly true with loops since each loop counts twice in the degree). The result is thus twice the number of edges of the graph. The method for this proof is a little like counting a herd of sheep: let us count the legs and divide the result by four (although for sheep there is always the question of five-legged sheep!). The following corollary, when applied in a different context from graphs, may appear far from self-evident.
Corollary 1.1.
In a graph the number of vertices with odd degrees is even.
Proof.
The sum of the degrees being even, since it is equal to twice the number of edges, can only include an even number of odd terms. Therefore,
there is an even number of odd degrees in the graph.
Here is an amusing application of this corollary. Let us imagine a group of nine friends who either shake hands or give each other hugs as a greeting in the morning. Each one of them shakes the hand of three of his friends and hugs the other five. This is in fact impossible! Let us model the situation of these friends by a graph which could be called “the hugging graph”: the vertices are the friends and two vertices are linked by an edge if and only if the related friends greet each other with a hug (this is a simple graph, in particular because no friend is assumed to greet himself). Any vertex is of degree 5 and there are nine vertices. This contradicts the preceding corollary.
The minimum degree of a graph G is the smallest degree of its vertices and is denoted by δG or simply δ. It should be observed that δG is the degree of at least one of the vertices of the graph. Likewise the maximum degree of G is the largest degree of its vertices and is denoted by ΔG or simply Δ. This is also the degree on at least one of the vertices of the graph.
Note. The following inequalities result from proposition 1.1:

1-Graph Theory and Applications ,Jean-Claude Fournier, WILEY, page(33-35)
2-Introduction to Graph Theory Second Edition, Douglas B. West , Indian Reprint, 2002,page(34)
 الاكثر قراءة في نظرية البيان
الاكثر قراءة في نظرية البيان
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















