
Matchings
 المؤلف:
John M. Harris • Jeffry L. Hirst • Michael J. Mossinghoff
المؤلف:
John M. Harris • Jeffry L. Hirst • Michael J. Mossinghoff
 المصدر:
Combinatorics and Graph Theory, Second Edition
المصدر:
Combinatorics and Graph Theory, Second Edition
 الجزء والصفحة:
101-104
الجزء والصفحة:
101-104
 3-8-2016
3-8-2016
 1944
1944
A matching in a graph is a set of independent edges. That is, it is a set of edges in which no pair shares a vertex. Given a matching M in a graph G, the vertices belonging to the edges of M are said to be saturated by M (or M-saturated). The other vertices are M-unsaturated.
Consider the graph G shown in Figure 1.1. An example of a matching in G is M1 = {ab, ce, df}. M2 = {cd, ab} is also a matching, and so is M3 = {df}.
We can see that a, b, c, d are M2-saturated and e, f,and g are M2-unsaturated. The onlyM1-unsaturated vertex is g.
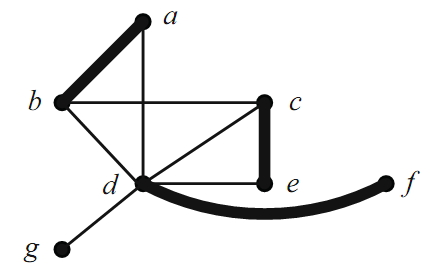
FIGURE 1.1. The matching M1.
If a matching M saturates every vertex of G,then M is said to be a perfect matching. In Figure 1.104, G1 has a perfect matching, namely {ab,ch,de,fg}.
None of G2, G3,and G4 has a perfect matching. Why is this? We will talk more about perfect matchings in Sectionof Perfect Matchings.
A maximum matching in a graph is a matching that has the largest possible cardinality. A maximal matching is a matching that cannot be enlarged by the
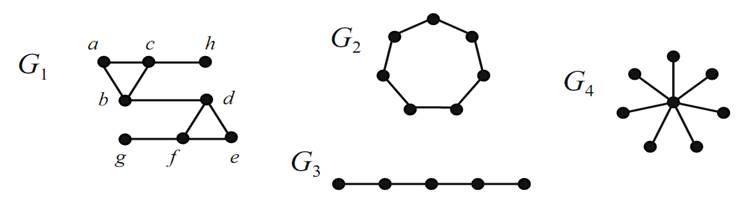
FIGURE 1.2. Only G1 has a perfect matching
addition of any edge. In Figure 1.3, M1 = {ae,bf,cd,gh} is a maximum matching (since at most one of gh, gi,and gj can be in any matching). The matching M2 = {dg, af, bc} is maximal, but not maximum.
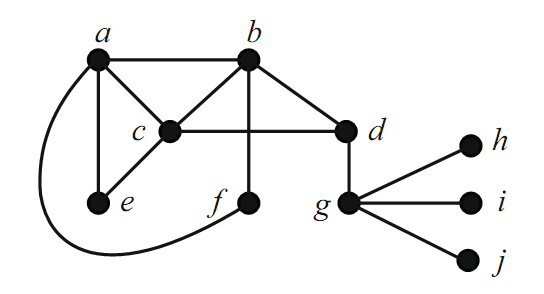
FIGURE 1.3.
Combinatorics and Graph Theory, Second Edition, John M. Harris • Jeffry L. Hirst • Michael J. Mossinghoff,2000,page(101-104)
 الاكثر قراءة في نظرية البيان
الاكثر قراءة في نظرية البيان
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


