
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Plane Wave in Dielectric
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 65
11-8-2016
1968
Plane Wave in Dielectric
A monochromatic plane wave of frequency ω propagates through a non-permeable (μ = 1) insulating medium with dielectric constant ε1. The wave is normally incident upon an interface with a similar medium with dielectric constant ε2 (see Figure 1.1).
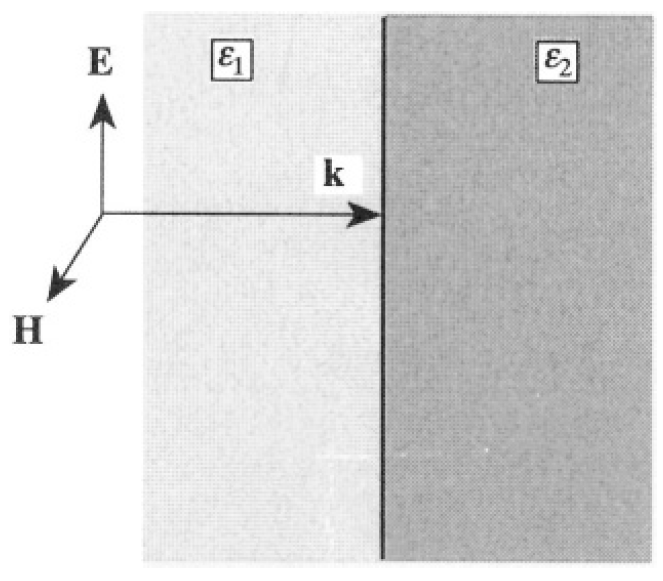
Figure 1.1
a) Derive the boundary conditions for the electric and magnetic fields at the interface.
b) Find the fraction of incident energy that is transmitted to the second medium.
SOLUTION
a) We assume that the dielectric constant is essentially real (no dissipation). For a monochromatic wave travelling in the z direction with E = E0ei(kz-ωt) we can write the sourceless Maxwell equations
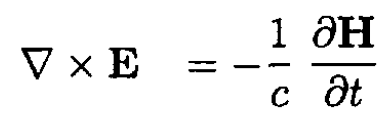 (1)
(1)
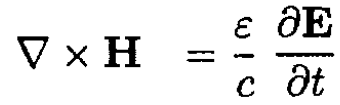 (2)
(2)
Substituting the explicit form for E (and H) produces the following exchange:
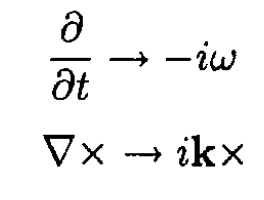
So (1) and (2) become
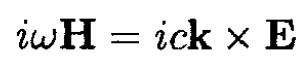 (3)
(3)
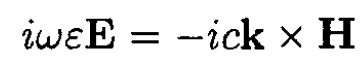 (4)
(4)
Orient the axes so that and 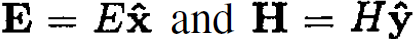 (see Figure 1.2). Then, the boundary conditions (which require continuity for the tangential components of E and H) become
(see Figure 1.2). Then, the boundary conditions (which require continuity for the tangential components of E and H) become

where the indices 1 and 2 correspond to dielectric media 1 and 2 (see Figure
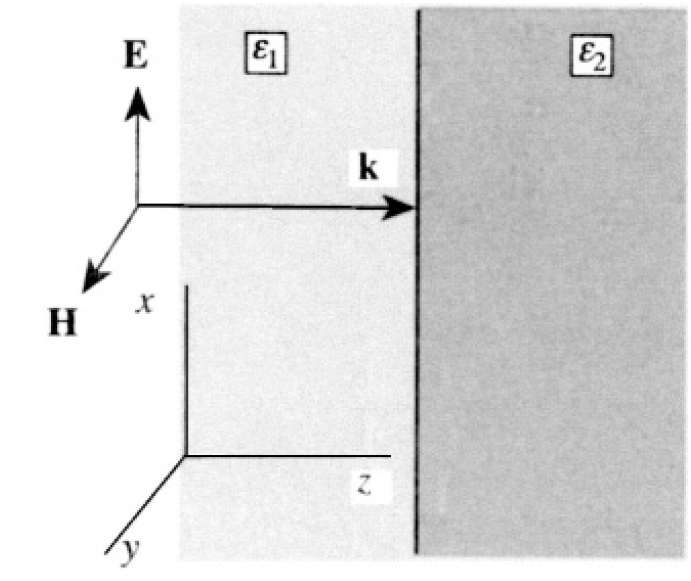
Figure 1.2
1.2). From (3),
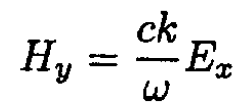 (5)
(5)
The field in medium 1 is the sum of the incident wave E0 and the reflected wave E1, whereasthe field in medium 2 is due only to the transmitted wave E2. Using the boundary conditions and (5), we obtain
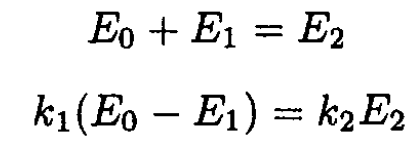 (6)
(6)
Solving (6) for E1 and E2,
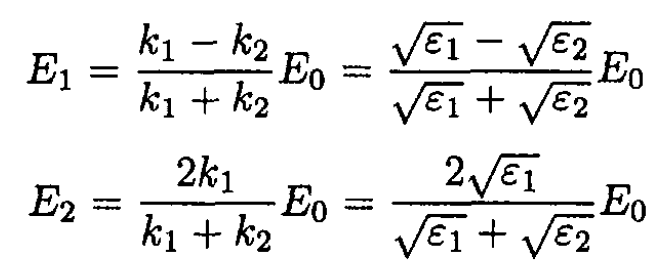 (7)
(7)
b) The energy flux in a monochromatic wave is given by the magnitude of the Poynting vector,
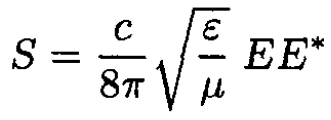 (8)
(8)
So the incident and transmitted fluxes S0 and S2, respectively, are, from (7)
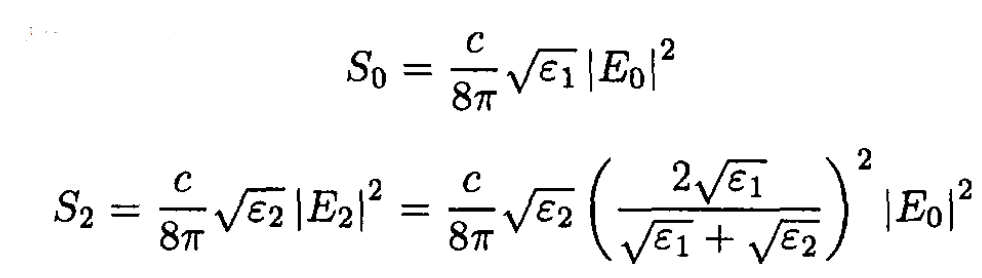
The fraction of the energy transmitted into the second medium is
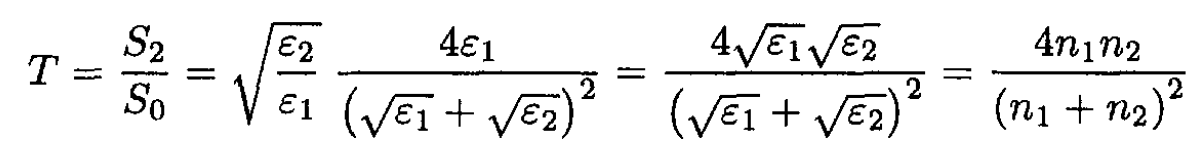 (9)
(9)
where we have substituted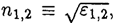 the indices of refraction of the two media. Similarly, the fraction of the energy reflected back into the first medium
the indices of refraction of the two media. Similarly, the fraction of the energy reflected back into the first medium
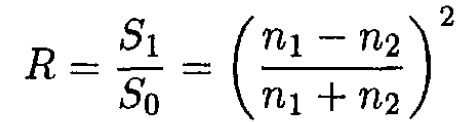 (10)
(10)
where S1 is the magnitude of the Poynting vector for the reflected wave. We can check that T + R = 1 by adding (9) and (10).
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















