


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | CIRCUITS FOR ARITHMETIC COMPUTATION-Subtraction of binary numbers. |
|
|
|
Read More
Date: 29-12-2016
Date: 28-12-2016
Date: 10-1-2017
|
The design of a circuit for subtraction is very similar to the problem of design for addition. The differences are primarily that the inputs must be distinguished as to order and, instead of a carry signal, it is necessary to indicate a borrow signal. Table 1-1 indicates the operation which must be performed by a circuit element we will term a half subtracter. The symbolic notation to be used in circuit diagrams is given in Fig. 1-1. We must distinguish between the two inputs. The plus sign will denote the minuend digit, and the minus sign will denote the digit from the subtrahend. The outputs will show the difference digit and the borrow digit.
TABLE 1-1
SUBTRACTION OF BINARY NUMBERS
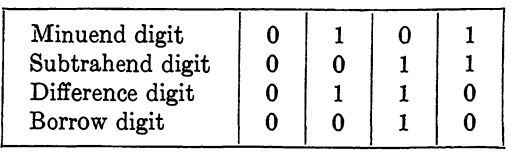
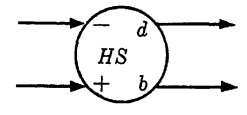
FIG. 1-1. Symbolic notation for a half subtracter.
To design a half subtracter, we note by consulting Table 1-1 that the function representing the difference output is given by d = xy' + x'y if x and y represent the two inputs. The order of the inputs is immaterial for the difference output, but to determine the borrow output an order must be stated. We will specify x as minuend digit and y as subtrahend digit. Then the borrow output is given by b = x'y. From these functions, the half subtracter can be designed immediately, as shown in Fig. 1-1.
Note that the circuit for the difference in a half subtracter is identical to the circuit for the sum in a half adder.
Now, using the half subtracter and the "or" element just as was done in the preceding section on addition, a logical circuit can be designed which will subtract two binary numbers. We will let the minuend be a 3-digit number X = x3x2x1. (The restriction to three digits is only for simplicity of illustration. Any number of digits can be handled in the same way.) The subtrahend Y = y3,y2,y1 will be a number of not more than three digits, which we will assume does not exceed the minuend in size. The difference of the two digits is given as the number D = d3d2d1, represented by the outputs of the circuit.

FIG. 1-1. Logical circuit for a half subtracter.
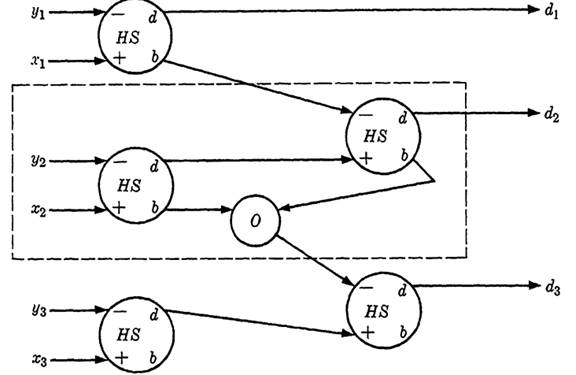
FIG. 1-2. Circuit for the subtraction of two 3-digit numbers.
sented by the outputs of the circuit. The diagram is given in Fig. 1-2. The unit which combines the second digits is the typical unit. This part of the circuit is enclosed in a broken line. If larger numbers are to be combined, this portion of the diagram is repeated for all number positions except the first and last, which are modified as in the diagram for 3-digit numbers.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
ملاكات العتبة العباسية تستقبل الزائرين بالتهاني في ذكرى ولادة الإمام علي (عليه السلام)
|
|
|