
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Magnetic energy
المؤلف:
Richard Fitzpatrick
المصدر:
Classical Electromagnetism
الجزء والصفحة:
p 196
9-1-2017
1868
Magnetic energy
Suppose that at t = 0 a coil of inductance L and resistance R is connected across the terminals of a battery of e.m.f. V . The circuit equation is
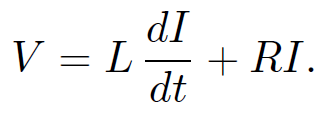 (1.1)
(1.1)
The power output of the battery is V I. [Every charge q that goes around the circuit falls through a potential difference qV . In order to raise it back to the starting potential, so that it can perform another circuit, the battery must do work qV. The work done per unit time (i.e., the power) is nqV , where n is the number of charges per unit time passing a given point on the circuit. But, I = nq, so the power output is V I.] The total work done by the battery in raising the current in the circuit from zero at time t = 0 to IT at time t = T is
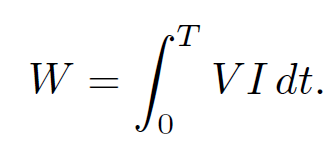 (1.2)
(1.2)
Using the circuit equation (1.1), we obtain
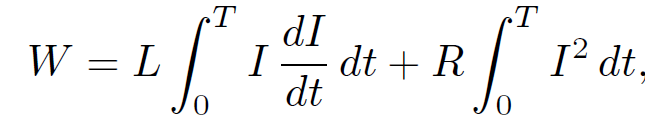 (1.3)
(1.3)
giving
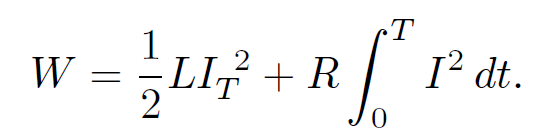 (1.4)
(1.4)
The second term on the right-hand side represents the irreversible conversion of electrical energy into heat energy in the resistor. The first term is the amount of energy stored in the inductor at time T. This energy can be recovered after the inductor is disconnected from the battery. Suppose that the battery is disconnected at time T. The circuit equation is now
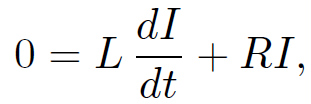 (1.5)
(1.5)
giving
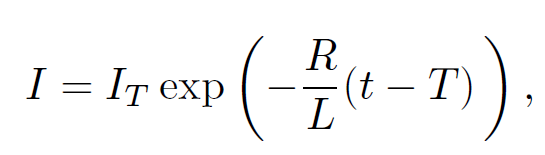 (1.6)
(1.6)
where we have made use of the boundary condition I(T) = IT . Thus, the current decays away exponentially. The energy stored in the inductor is dissipated as heat in the resistor. The total heat energy appearing in the resistor after the battery is disconnected is
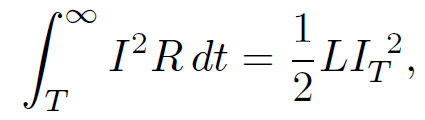 (1.7)
(1.7)
where use has been made of Eq. (1.6). Thus, the heat energy appearing in the resistor is equal to the energy stored in the inductor. This energy is actually stored in the magnetic field generated around the inductor. Consider, again, our circuit with two coils wound on top of one another. Suppose that each coil is connected to its own battery. The circuit equations are
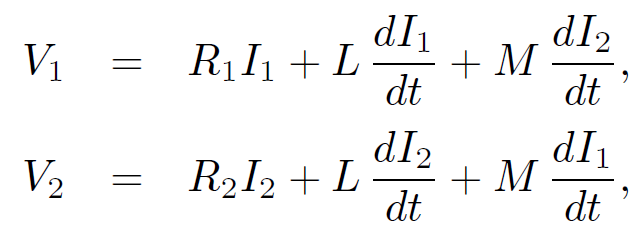 (1.8)
(1.8)
where V1 is the e.m.f. of the battery in the first circuit, etc. The work done by the two batteries in increasing the currents in the two circuits from zero at time 0 to I1 and I2 at time T, respectively, is
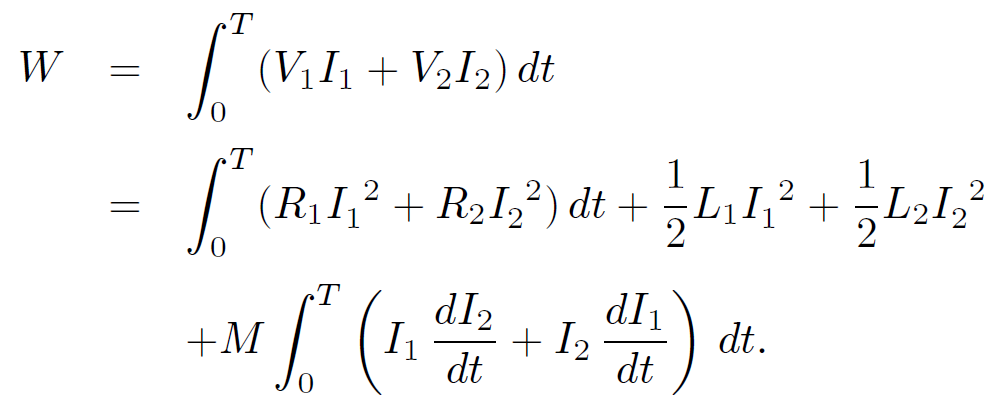 (1.9)
(1.9)
Thus,
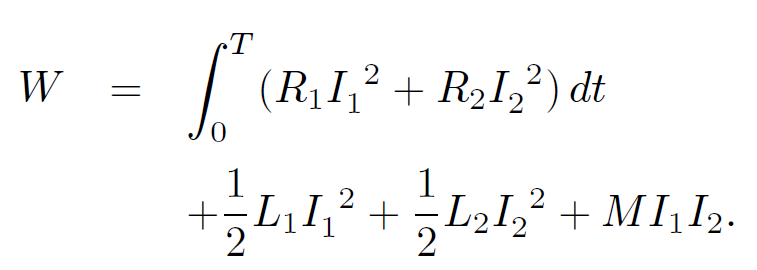 (1.10)
(1.10)
Clearly, the total magnetic energy stored in the two coils is
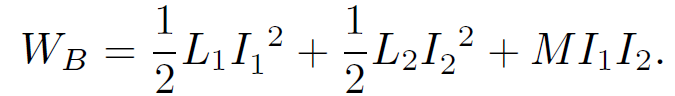 (1.11)
(1.11)
Note that the mutual inductance term increases the stored magnetic energy if I1 and I2 are of the same sign i.e., if the currents in the two coils flow in the same direction, so that they generate magnetic fields which reinforce one another. Conversely, the mutual inductance term decreases the stored magnetic energy if I1 and I2 are of the opposite sign. The total stored energy can never be negative, otherwise the coils would constitute a power source (a negative stored energy is equivalent to a positive generated energy). Thus,
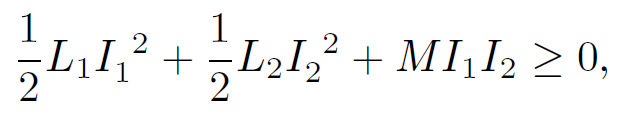 (1.12)
(1.12)
which can be written
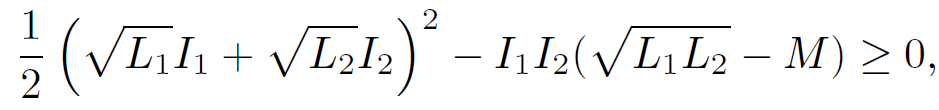 (1.13)
(1.13)
assuming that I1I2 < 0. It follows that
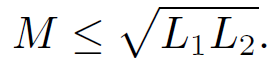 (1.14)
(1.14)
The equality sign corresponds to the situation where all of the flux generated by one coil passes through the other. If some of the flux misses then the inequality sign is appropriate. In fact, the above formula is valid for any two inductively coupled circuits. We intimated previously that the energy stored in an inductor is actually stored in the surrounding magnetic field. Let us now obtain an explicit formula for the energy stored in a magnetic field. Consider an ideal solenoid. The energy stored in the solenoid when a current I flows through it is
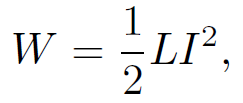 (1.15)
(1.15)
where L is the self-inductance. We know that
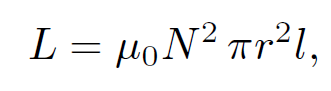 (1.16)
(1.16)
where N is the number of turns per unit length of the solenoid, r the radius, and l the length. The field inside the solenoid is uniform, with magnitude
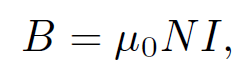 (1.17)
(1.17)
and is zero outside the solenoid. Equation (1.15) can be rewritten
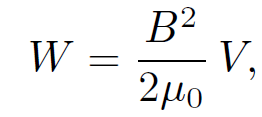 (1.18)
(1.18)
where V = πr2l is the volume of the solenoid. The above formula strongly suggests that a magnetic field possesses an energy density
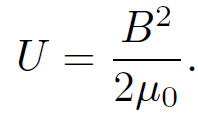 (1.19)
(1.19)
Let us now examine a more general proof of the above formula. Consider a system of N circuits (labeled i = 1 to N), each carrying a current Ii. The magnetic flux through the ith circuit is written
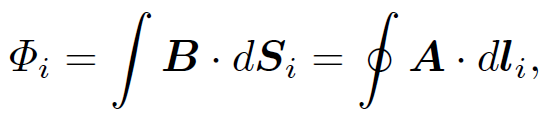 (1.20)
(1.20)
where B = ∇˄A, and dSi and dli denote a surface element and a line element of this circuit, respectively. The back e.m.f. induced in the ith circuit follows from Faraday's law:
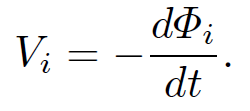 (1.21)
(1.21)
The rate of work of the battery which maintains the current Ii in the ith circuit against this back e.m.f. is
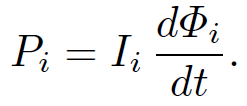 (1.22)
(1.22)
Thus, the total work required to raise the currents in the N circuits from zero at time 0 to I0i at time T is
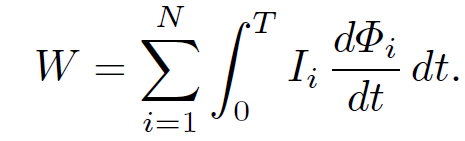 (1.23)
(1.23)
The above expression for the work done is, of course, equivalent to the total energy stored in the magnetic field surrounding the various circuits. This energy is independent of the manner in which the currents are set up. Suppose, for the sake of simplicity, that the currents are ramped up linearly, so that
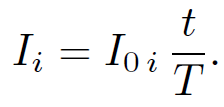 (1.24)
(1.24)
The fluxes are proportional to the currents, so they must also ramp up linearly:
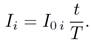 (1.25)
(1.25)
It follows that
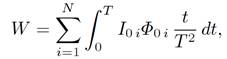 (1.26)
(1.26)
giving
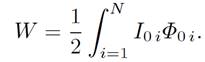 (1.27)
(1.27)
So, if instantaneous currents Ii flow in the N circuits, which link instantaneous fluxes ɸi, then the instantaneous stored energy is
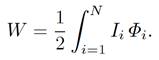 (1.28)
(1.28)
Equations (1.20) and (1.28) imply that
 (1.29)
(1.29)
It is convenient, at this stage, to replace our N line currents by N current distributions of small, but finite, cross-sectional area. Equation (1.29) transforms to
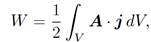 (1.30)
(1.30)
where V is a volume which contains all of the circuits. Note that for an element of the ith circuit j = Ii dli=dliAi and dV = dliAi, where Ai is the cross-sectional area of the circuit. Now, μ0j = ∇˄B (we are neglecting the displacement current in this calculation), so
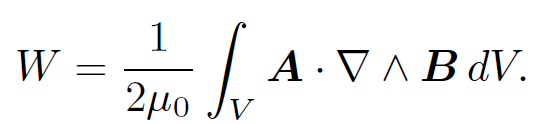 (1.31)
(1.31)
According to vector field theory,
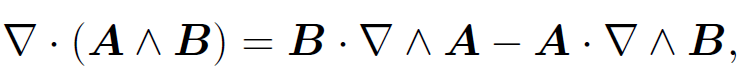 (1.32)
(1.32)
which implies that
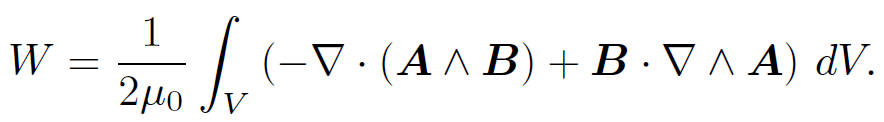 (1.33)
(1.33)
Using Gauss' theorem and B = ∇˄ A, we obtain
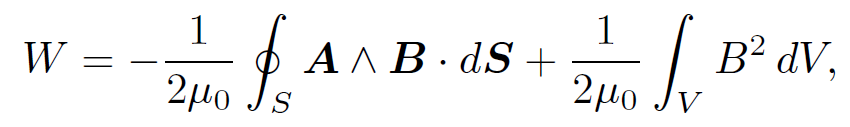 (1.34)
(1.34)
where S is the bounding surface of V . Let us take this surface to infinity. It is easily demonstrated that the magnetic field generated by a current loop falls of like r-3 at large distances. The vector potential falls o® like r-2. However, the area of surface S only increases like r2. It follows that the surface integral is negligible in the limit r → ∞. Thus, the above expression reduces to
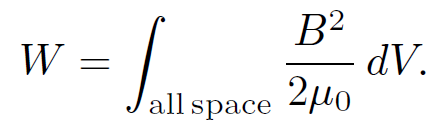 (1.35)
(1.35)
Since this expression is valid for any magnetic field whatsoever, we can conclude that the energy density of a general magnetic field is given by
 (1.36)
(1.36)
 الاكثر قراءة في المغناطيسية
الاكثر قراءة في المغناطيسية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















