


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-1-2019
Date: 21-1-2019
Date: 9-3-2017
|
An asymptote is, essentially, a line that a graph approaches, but does not intersect. For example, in the following graph of y=1/x, the line approaches the x-axis (y=0), but never touches it. No matter how far we go into infinity, the line will not actually reach y=0, but will always get closer and closer.
y=1/x:
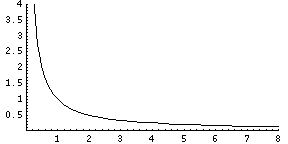
This means that the line y=0 is a horizontal asymptote. Horizontal asymptotes occur most often when the function is a fraction where the top remains positive, but the bottom goes to infinity. Going back to the previous example, y=1/x is a fraction. When we go out to infinity on the x-axis, the top of the fraction remains 1, but the bottom gets bigger and bigger. As a result, the entire fraction actually gets smaller, although it will not hit zero. The function will be 1/2, then 1/3, then 1/10, even 1/10000, but never quite 0. Thus, y=0 is a horizontal asymptote for the function y=1/x.
Here is another example, y=(4x+2)/(x^2+1):
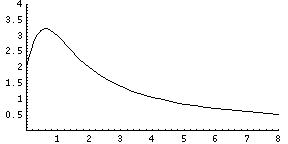
As you can see in the above graph, the equation approaches zero eventually. This happens because on the top of the fraction 4x+2 will always be positive, but the denominator, x^2+1, will be far larger. Because the bottom will dominate the top, the fraction approaches zero as x gets closer to infinity. This equation also has an asymptote at y=0.
Now let's find an example with an asymptote not located at y=0. Here is the graph of y=3x/(x+2):
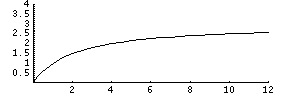
Now, examine what happens when x approaches infinity. The denominator of the fraction is x+2, and as x gets really huge that +2 is meaningless (what's the difference in 100000 and 100002?), so we can forget the +2. Now our equation looks like this:
y=3x/x.
Cancel out the x's, and you have y=3. You just took the limit as x approached infinity and discovered that the asymptote is y=3. When x gets to infinity, y is getting really really close to 3. To find horizontal asymptotes, simply look to see what happens when x goes to infinity.
The second type of asymptote is the vertical asymptote, which is also a line that the graph approaches but does not intersect. Vertical asymptotes almost always occur because the denominator of a fraction has gone to 0, but the top hasn't. For example, y=4/(x-2):
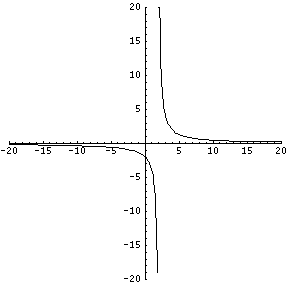
Note that as the graph approaches x=2 from the left, the curve drops rapidly towards negative infinity. This is because the numerator is staying at 4, and the denominator is getting close to 0. That means that the fraction itself is getting very big and negative. When x is exactly 2, the function does not exist because you cannot divide by 0. Immediately after 2 it resumes at positive infinity, because the numerator is 4 and the denominator is again very tiny, but this time it is positive.
To find vertical asymptotes, look for any circumstance that makes the denominator of a fraction equal zero. Those are the most likely candidates, at which point you can graph the function to check, or take the limit to see how the graph behaves as it approaches the possible asymptote.
Also keep in mind that trigonometric functions can go to zero repeatedly, so in the equation y=sec(x), there are many vertical asymptotes:

All of those vertical lines are really asymptotes, which brings up a good point. Your calculator or computer will most likely draw asymptotes as black lines that look like the rest of the graph. This is because the computer wants to connect all the points, and it is not as smart as you. You must use your own judgement to recognize asymptotes when you see a computerized graph.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|