


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-3-2017
Date: 30-3-2017
Date: 25-3-2017
|
Died: 24 January 1955 in Durham, England
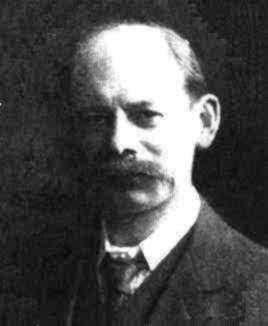
P J Heawood's father was the Reverend John Richard Heawood. He had a brother, Edward Heawood, who went on to become librarian for the Royal Geographical Society, holding the position for over 30 years.
Heawood attended Queen Elizabeth's Grammar School in Ipswich being awarded an Open Scholarship to study at Exeter College, Oxford, in 1880. There Heawood was most influenced by Henry Smith and he went on to be a Wrangler in 1883 (the year in which Henry Smith died).
Heawood was awarded a Junior Mathematical Scholarship in 1882 and a Senior Mathematical Scholarship in 1886. In 1886 he was also awarded the Lady Herschell Prize.
In 1887 Heawood was appointed Lecturer in Mathematics at Durham Colleges (later Durham University). Three years later, in June 1890, he married Christiana Tristram who was the daughter of Canon H B Tristram who was a biblical scholar, traveller and naturalist. They had a son and a daughter and enjoyed over sixty years of marriage, celebrating their diamond wedding in June 1950.
In fact Heawood worked at Durham University all his life being appointed to the Chair of Mathematics there in 1911. He served the university in many capacities, in particular he was a member of the Senate from 1905 and served as Vice-Chancellor from 1926 to 1928. He did not retire until 1939 when he was 78 years of age but still went on to enjoy 16 years of retirement.
Heawood spent 60 years of his life working on the four colour theorem. He published his first paper on the topic Map colour theorems in 1890 when he pointed out the mistake in Kempe's proof. In the same paper he proves that five colours suffice. He also proved in this paper that for a surface of connectivity h, a map requires at most
[7/2 + √(24h - 23))/2]
colours. Another result from the same paper considered empires, countries which have a number of colonies which must all be coloured with the same colour. Heawood proved that if an empire contains at most r disjoint portions then on a surface of connectivity h, a map can be coloured with at most
{6r + 1 + √(24h +(6r + 1)2- 72)}/2
colours. He gave a map with 12 countries, each in two disjoint parts, which required 12 colours.
Heawood wrote on the four colour problem again in 1897, 1932, 1936, 1943, 1944 and his final paper on the topic in 1949 was given the same title Map colour theorems as his first paper.
Other topics which Heawood wrote on were continued fractions, approximation theory, and quadratic residues. He also wrote five papers and 23 notes for the Mathematical Gazette on a variety of mathematical topics but perhaps more on geometry than any other topic.
Dirac, in [2], describes Heawood's appearance and character in the following words:-
In his appearance, manners and habits of thought, Heawood was an extravagantly unusual man. He had an immense moustache and a meagre, slightly stooping figure. He usually wore an Inverness cape of strange pattern and manifest antiquity, and carried an ancient handbag. His walk was delicate and hasty, and he was often accompanied by a dog, which was admitted to his lectures. ... His transparent sincerity, piety and goodness of heart, and his eccentricity and extraordinary blend of naiveté and shrewdness secured for him not only the fascinated interest, but also the regard and respect of his colleagues.
Heawood had one passion outside mathematics and university life. In 1928 Durham Castle was found to be insecure with the foundations moving on the cliff on which it was built. Very large amounts of money were required to save the castle and the University of Durham failed in its attempt to raise the necessary money. Heawood however refused to give up and for years he worked almost on his own as Secretary of the Durham Castle Restoration Fund to raise the cash.
Without Heawood's efforts Durham Castle would not be standing today. He succeeded against all the odds to raise the money necessary to ensure that the foundations were permanently secured. He received the O.B.E. in 1939 for this work.
Heawood's other interests are mentioned in [1]:-
... he was fond of country pursuits, and one of his interests, unusual for a mathematician, was Hebrew.
Articles:



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل: شراكتنا مع المؤسّسات الرائدة تفتح آفاقًا جديدة للارتقاء بجودة التعليم الطبّي في العراق
|
|
|