


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | Covering Maps and Discontinuous Group Actions-Discontinuous Group Actions |
|
|
|
Read More
Date: 23-5-2021
Date: 1-6-2021
Date: 24-6-2017
|
Definition Let G be a group, and let X be a set. The group G is said to act on the set X (on the left) if each element g of G determines a corresponding function θg: X → X from the set X to itself, where
(i) θgh = θg ◦ θh for all g, h ∈ G;
(ii) the function θe determined by the identity element e of G is the identity function of X.
Let G be a group acting on a set X. Given any element x of X, the orbit [x]G of x (under the group action) is defined to be the subset {θg(x) : g ∈ G} of X, and the stabilizer of x is defined to the the subgroup {g ∈ G : θg(x) =x} of the group G. Thus the orbit of an element x of X is the set consisting of all points of X to which x gets mapped under the action of elements of the group G. The stabilizer of x is the subgroup of G consisting of all elements of this group that fix the point x. The group G is said to act freely on X if θg(x) ≠x for all x ∈ X and g ∈ G satisfying g ≠e. Thus the group G acts freely on X if and only if the stabilizer of every element of X is the trivial subgroup of G.
Let e be the identity element of G. Then x = θe(x) for all x ∈ X, and therefore x ∈ [x]G for all x ∈ X, where [x]G = {θg(x) : g ∈ G}.
Let x and y be elements of G for which [x]G ∩ [y]G is non-empty, and let z ∈ [x]G ∩ [y]G. Then there exist elements h and k of G such that z = θh(x) = θk(y). Then θg(z) = θgh(x) = θgk(y), θg(x) = θgh−1 (z) and θg(y) = θgk−1 (z) for all g ∈ G, and therefore [x]G = [z]G = [y]G. It follows from this that the group action partitions the set X into orbits, so that each element of X determines an orbit which is the unique orbit for the action of G on X to which it belongs. We denote by X/G the set of orbits for the action of G on X.
Now suppose that the group G acts on a topological space X. Then there is a surjective function q: X → X/G, where q(x) = [x]G for all x ∈ X.
This surjective function induces a quotient topology on the set of orbits: a subset U of X/G is open in this quotient topology if and only if q−1 (U) is an open set in X. We define the orbit space X/G for the action of G on X to be the topological space whose underlying set is the set of orbits for the action of G on X, the topology on X/G being the quotient topology induced by the function q: X → X/G. This function q: X → X/G is then an identification map: we shall refer to it as the quotient map from X to X/G.
We shall be concerned here with situations in which a group action on a topological space gives rise to a covering map. The relevant group actions are those where the group acts freely and properly discontinuously on the topological space
Definition Let G be a group with identity element e, and let X be a topological space. The group G is said to act freely and properly discontinuously on X if each element g of G determines a corresponding continuous map θg: X → X, where the following conditions are satisfied:
(i) θgh = θg ◦ θh for all g, h ∈ G;
(ii) the continuous map θe determined by the identity element e of G is the identity map of X;
(iii) given any point x of X, there exists an open set U in X such that x ∈ U and θg(U) ∩ U = ∅ for all g ∈ G satisfying g ≠e.
Let G be a group which acts freely and properly discontinuously on a topological space X. Given any element g of G, the corresponding continuous function θg: X → X determined by X is a homeomorphism. Indeed it follows from conditions (i) and (ii) in the above definition that θg−1 ◦ θg and θg ◦ θg−1 are both equal to the identity map of X, and therefore θg: X → X is a homeomorphism with inverse θg−1 : X → X.
Remark The terminology `freely and properly discontinuously' is traditional, but is hardly ideal. The adverb ‘freely’ refers to the requirement that θg(x) ≠x for all x ∈ X and for all g ∈ G satisfying g ≠ e. The adverb ‘discontinuously’ refers to the fact that, given any point x of G, the elements of the orbit {θg(x) : g ∈ G} of x are separated; it does not signify that the functions defining the action are in any way discontinuous or badly-behaved. The adverb ‘properly’ refers to the fact that, given any compact subset K of X, the number of elements of g for which K θg(K) ≠θ is finite. Moreover the definitions of properly discontinuous actions in textbooks and in sources of reference are not always in agreement: some say that an action of a group G on a topological space X (where each group element determines a corresponding homeomorphism of the topological space) is properly discontinuous if, given any x ∈ X, there exists an open set U in X such that the number of elements g of the group for which g(U)∩U ≠ ∅ is finite; others say that the action is properly discontinuous if it satisfies the conditions given in the definition above for a group acting freely and properly discontinuously on the set. William Fulton, in his textbook Algebraic topology: a first course (Springer, 1995), introduced the term `evenly' in place of `freely and properly discontinuously', but this change in terminology does not appear to have been generally adopted.
Proposition 1.8 Let G be a group acting freely and properly discontinuously on a topological space X. Then the quotient map q: X → X/G from X to the corresponding orbit space X/G is a covering map.
Proof The quotient map q: X → X/G is surjective. Let V be an open set in X. Then q−1(q(V )) is the union Sg∈Gθg(V ) of the open sets θg(V ) as g ranges over the group G, since q−1 (q(V )) is the subset of X consisting of all elements of X that belong to the orbit of some element of V . But any union of open sets in a topological space is an open set. We conclude therefore that if V is an open set in X then q(V ) is an open set in X/G.
Let x be a point of X. Then there exists an open set U in X such that x ∈ U and θg(U) ∩ U = ∅ for all g ∈ G satisfying g ≠ e. Now q−1 (q(U)) =Sg∈Gθg(U). We claim that the sets θg(U) are disjoint. Let g and h be elements of G. Suppose that θg(U)∩θh(U) ≠ ∅. Then θh−1 (θg(U)∩θh(U)) ≠ ∅. But θh−1 : X → X is a bijection, and therefore θh−1 (θg(U) ∩ θh(U)) = θh−1 (θg(U)) ∩ θh−1 (θh(U)) = θh−1g(U) ∩ U, and therefore θh−1g(U) ∩ U ≠∅. It follows that h−1g = e, where e denotes the identity element of G, and therefore g = h. Thus if g and h are elements of g, and if g ≠ h, then θg(U) ∩ θh(U) = ∅. We conclude therefore that the preimage q−1(q(U)) of q(U) is the disjoint union of the sets θg(U) as g ranges over the group G. Moreover each these sets θg(U) is an open set in X.
Now U ∩ [u]G = {u} for all u ∈ U, since [u]G = {θg(u) : g ∈ G} and U ∩ θg(U) = ∅ when g ≠e. Thus if u and v are elements of U, and if q(u) =q(v) then [u]G = [v]G and therefore u = v. It follows that the restriction q|U: U → X/G of the quotient map q to U is injective, and therefore q maps U bijectively onto q(U). But q maps open sets onto open sets, and any continuous bijection that maps open sets onto open sets is a homeomorphism.
We conclude therefore that the restriction of q: X → X/G to the open set U maps U homeomorphically onto q(U). Moreover, given any element g of G,
the quotient map q satisfies q = q ◦ θg−1 , and the homeomorphism θg−1 maps θg(U) homeomorphically onto U. It follows that the quotient map q maps θg(U) homeomorphically onto q(U) for all g ∈ U. We conclude therefore that q(U) is an evenly covered open set in X/G whose preimage q−1 (q(U)) is the disjoint union of the open sets θg(U) as g ranges over the group G. It follows that the quotient map q: X → X/G is a covering map, as required.
Theorem 1.9 Let G be a group acting freely and properly discontinuously on a path-connected topological space X, let q: X → X/G be the quotient map from X to the orbit space X/G, and let x0 be a point of X. Then there exists a surjective homomorphism λ: π1(X/G, q(x0)) → G with the property that γ˜(1) = θλ([γ])(x0) for any loop γ in X/G based at q(x0), where γ˜ denotes the unique path in X for which γ˜(0) = x0 and q ◦ γ˜ = γ. The kernel of this homomorphism is the subgroup q#(π1(X, x0)) of π1(X/G, q(x0)).
Proof Let γ: [0, 1] → X/G be a loop in the orbit space with γ(0) = γ(1) =q(x0). It follows from the Path Lifting Theorem for covering maps (Path Lifting Theorem) that there exists a unique path γ˜: [0, 1] → X for which γ˜ (0) = x0 and q ◦ γ˜ = γ. Now γ˜ (0) and γ˜ (1) must belong to the same orbit, since q(γ˜ (0)) = γ(0) = γ(1) = q(γ˜(1)). Therefore there exists some element g of G such that γ˜(1) = θg(x0). This element g is uniquely determined, since the group G acts freely on X. Moreover the value of g is determined by the based homotopy class [γ] of in π1 (X,q(x0)). Indeed it follows from Proposition 1.1 that if σ is a loop in X/G based at q(x0), if σ˜ is the lift of σ starting at x0 (so that q ◦σ˜ = σ and σ˜ (0) = x0), and if [γ] = [σ] in π1(X/G, q(x0)) (so that γ ≃ σ rel {0, 1}), then γ˜ (1) = σ˜(1). We conclude therefore that there exists a well-defined function
λ: π1(X/G, q(x0)) → G,
which is characterized by the property that γ˜ (1) = θλ([γ])(x0) for any loop γ in X/G based at q(x0), where γ˜ denotes the unique path in X for which γ˜(0) = x0 and q ◦ γ˜ = γ.
Now let α: [0, 1] → X/G and β: [0, 1] → X/G be loops in X/G based at x0, and let α˜: [0, 1] → X and β˜: [0, 1] → X be the lifts of α and β respectively starting at x0, so that q ◦ α˜ = α, q ◦ β˜ = β and α˜(0) = β˜(0) = x0. Thenα˜(1) = θλ([α])(x0) and β˜(1) = θλ([β])(x0). Then the path θλ([α]) ◦ β˜ is also a lift of the loop β, and is the unique lift of β starting at α˜ (1). Let α.β be the concatenation of the loops α and β, where
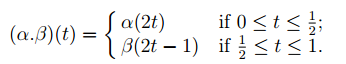
Then the unique lift of α.β to X starting at x0 is the path σ: [0, 1] → X, where
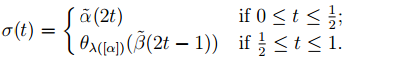
It follows that
θλ([α][β])(x0) = θλ([α.β])(x0) = σ(1) = θλ([α])(β˜(1))
= θλ([α])(θλ([β])(x0)) = θλ([α])λ([β])(x0)
and therefore λ([α][β]) = λ([α])λ([β]). Therefore the function
λ: π1(X/G, q(x0)) → G
is a homomorphism.
Let g ∈ G. Then there exists a path α in X from x0 to θg(x0), since the space X is path-connected. Then q ◦ α is a loop in X/G based at q(x0), and g = λ([q ◦ α]). This shows that the homomorphism λ is surjective.
Let γ: [0, 1] → X/G be a loop in X/G based at q(x0). Suppose that [γ] ∈ ker λ. Then γ˜(1) = θe(x0) = x0, and therefore γ˜ is a loop in X based at x0. Moreover [γ] = q#[γ˜], and therefore [γ] ∈ q#(π1(X, x0)). On the other hand, if [γ] ∈ q#(π1(X, x0)) then γ = q ◦ γ˜ for some loop γ˜ in X based at x0 (see Corollary 1.3). But then x0 = γ˜ (1) = θλ([γ])(x0), and therefore λ([γ]) = e, where e is the identity element of G. Thus ker λ = q#(π1(X, x0)), as required.
Corollary 1.10 Let G be a group acting freely and properly discontinuously on a path-connected topological space X, let q: X → X/G be the quotient map from X to the orbit space X/G, and let x0 be a point of X. Then q#(π1(X, x0)) is a normal subgroup of the fundamental group π1(X/G, q(x0)) of the orbit space, and
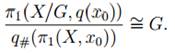
Proof The subgroup q#(π1(X, x0)) is the kernel of the homomorphism
λ: π1(X/G, q(x0)) → G
described in the statement of Theorem 1.9. It is therefore a normal subgroup of π1(X/G, q(x0)), since the kernel of any homomorphism is a normal subgroup. The homomorphism λ is surjective, and the image of any group homomorphism is isomorphism of the quotient of its domain by its kernel.
The result follows.
Corollary 1.11 Let G be a group acting freely and properly discontinuously on a simply-connected topological space X, let q: X → X/G be the quotient map from X to the orbit space X/G, and let x0 be a point of X. Then
π1(X/G, q(x0)) ≅ G.
Proof This is a special case of Corollary 1.10.
Example The group Z of integers under addition acts freely and properly discontinuously on the real line R. Indeed each integer n determines a corresponding homeomorphism θn: R → R, where θn(x) = x + n for all x ∈ R.
Moreover θm ◦ θn = θm+n for all m, n ∈ Z, and θ0 is the identity map of R. If U = (−1/2, 1/2) then θn(U) ∩ U = ∅ for all non-zero integers n. The real line R is simply-connected. It follows from Corollary 1.11 that π1(R/Z, b) ≅ Z for any point b of R/Z.
Now the orbit space R/Z is homeomorphic to a circle. Indeed let q: R →R/Z be the quotient map. Then the surjective function p: R → S1 which sends t ∈ R to (cos 2πt,sin 2πt) induces a continuous map h: R/Z → S1 defined on the orbit space which satisfies h ◦ q = p, since the quotient map q is an identification map. Moreover real numbers t1 and t2 satisfy p(t1) = p(t2) if and only if q(t1) = q(t2). It follows that the induced map h: R/Z → S1 is a bijection. This map also maps open sets to open sets, for if W is any open set in the orbit space R/Z then q−1(W) is an open set in R, and therefore p(q−1 (W)) is an open set in S1, since the covering map p: R → S1 maps open sets to open sets. But p(q−1 (W)) = h(W) for all open sets W in R/Z. Thus the continuous bijection h: R/Z → S1 maps open sets to open sets, and is therefore a homeomorphism. Thus Corollary 1.11 generalizes the result of Theorem (π1(S1, b) ≅ Z for any b ∈ S1).
Example The group Zn of ordered n-tuples of integers under addition acts freely and properly discontinuously on Rn, where
θ(m1,m2,...,mn)(x1, x2, . . . , xn) = (x1 + m1, x2 + m2, . . . , xn + mn)
for all (m1, m2, . . . , mn) ∈ Zn and (x1, x2, . . . , xn) ∈ Rn . The orbit space Rn/Zn is an n-dimensional torus, homeomorphic to the product of n circles. It follows from Corollary 1.11 that the fundamental group of this n-dimensional torus is isomorphic to the group Zn.
Example Let C2 be the cyclic group of order 2. Then C2 = {e, a} where e is the identity element, a ≠e, a2 = e. Then the group C2 acts freely and properly discontinuously on the n-dimensional sphere Sn for each nonnegative integer n. We represent Sn as the unit sphere centred on the origin in Rn+1. The homeomorphism θe determined by the identity element e of C2 is the identity map of Sn; the homeomorphism θa determined by the element a of C2 is the antipodal map that sends each point x of Sn to −x.
The orbit space Sn/C2 is homeomorphic to real projective n-dimensional space RPn. The n-dimensional sphere is simply-connected if n > 1. It follows from Corollary 1.11 that the fundamental group of RPn is isomorphic to the cyclic group C2 when n > 1.
Note that S0 is a pair of points, and RP0 is a single point. Also S1is a circle (which is not simply-connected) and RP1 is homeomorphic to a circle. Moreover, for any b ∈ S1 , the homomorphism q#: π1(S1, b) → π1(RP1, q(b)) corresponds to the homomorphism from Z to Z that sends each integer n to 2n. This is consistent with the conclusions of Corollary 1.10 in this example.
Example Given a pair (m, n) of integers, let θm,n:R2→R2 be the homeomorphism of the plane R2 defined such that θm,n(x, y) = (x+m,(−1)my +n)
for all (x, y) ∈ R2. Let (m1, n1) and (m2, n2) be ordered pairs of integers.
Then θm1,n1 ◦θm2,n2 = θm1+m2,n1+(−1)m1n2 . Let Γ be the group whose elements are represented as ordered pairs of integers, where the group operation # on Γ is defined such that
(m1, n1)#(m2, n2) = (m1 + m2, n1 + (−1)m1 n2)
for all (m1, n1),(m2, n2) ∈ Γ. The group Γ is non-Abelian, and its identity element is (0, 0). This group acts on the plane R2: given (m, n) ∈ Γ thecorresponding symmetry θm,n is a translation if m is even, and is a glide reflection if m is odd. Given a pair (m, n) of integers, the corresponding homeomorphism θm,n maps an open disk about the point (x, y) onto an open
disk of the same radius about the point θ(m,n)(x, y). It follows that if D is the open disk of radius ½ about the point (x, y), and if D ∩ θm,n(D) is nonempty, then (m, n) = (0, 0). Thus the group Γ maps freely and properly discontinuously on the plane R2.
The orbit space R2/Γ is homeomorphic to a Klein bottle. To see this, note each orbit intersects the closed unit square S, where S = [0, 1] × [0, 1].
If 0 < x < 1 and 0 < y < 1 then the orbit of (x, y) intersects the square S in one point, namely the point (x, y). If 0 < x < 1, then the orbit of (x, 0) intersects the square in two points (x, 0) and (x, 1). If 0 < y < 1 then the orbit of (0, y) intersects the square S in the two points (0, y) and (1, 1 − y).
(Note that (1, 1−y) = θ1,1(0, y).) And the orbit of any corner of the square S intersects the square in the four corners of the square. The restriction q|S of the quotient map q: R
2 → R2/Γ to the square S is a continuous surjection defined on the square: one can readily verify that it is an identification map.
It follows that the orbit space R2/Γ is homeomorphic to the identification space obtained from the closed square S by identifying together the points (x, 0) and (x, 1) where the real number x satisfies 0 < x < 1, identifying together the points (0, y) and (1, 1 − y) where the real number y satisfies 0 < y < 1, and identifying together the four corners of the square: this identification space is the Klein bottle.
The plane R2 is simply-connected. It follows from Corollary 1.11 that the fundamental group of the Klein bottle is isomorphic to the group Γ defined above.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|