Let p: X˜ → X be a covering map over a topological space X. Let f:Z → X be a continuous map from some topological space Z into X. If the topological space Z is locally path-connected then one can formulate a criterion to determine whether or not there exists a map f˜:Z → X˜ for which p ◦f˜ = f  . This criterion is stated in terms of the homomorphisms of fundamental groups induced by the continuous maps f:Z → X and p: X˜ → X. We shall use this criterion in order to derive a necessary and sufficient condition for two covering maps over a connected and locally path-connected topological space to be topologically equivalent. We shall also study the deck transformations of a covering space over some connected and locally path-connected topological space.

Lemma 1.18 Let p: X˜ → X be a covering map over a topological space X,  let Z be a locally path-connected topological space, and let g:Z → X˜ be a function from Z to X˜. Suppose that p ◦ g:Z → X is continuous, and that g ◦ γ: [0, 1] → X˜ is continuous for all paths γ: [0, 1] → Z in Z. Then the function g is continuous.

Proof Let f:Z → X be the composition function p◦g. Then the function f is a continuous map from Z to X.

Let z be a point of Z. Then there exists an open neighbourhood V of f(z)  in X which is evenly covered by the map p. The inverse image p⁻¹ (V ) of V in the covering space X˜ is a disjoint union of open sets, each of which is mapped homeomorphically onto V by p. One of these open sets contains the point g(z), since f(z) = p(g(z)). Let us denote this open set by V˜ . Then g(z) ∈ V˜ , and V˜ is mapped homeomorphically onto V by the map p. Let s: V → V˜ denote the inverse of the restriction (p|V˜ ): V˜ → V of the covering map p to V˜ . Then the map s is continuous, and p(s(v)) = v for all v ∈ V .

Now f⁻¹ (V ) is an open set in Z containing the point z. But the topological space Z is locally path-connected. Therefore there exists a path-connected open set N_z in Z such that z ∈ N_z and N_z ⊂ f⁻¹ (V ). We claim that g(N_z) ⊂ V˜ . Let z΄ be a point of N_z. Then there exists a path γ: [0, 1] → N_z in N from z to z΄ . Moreover f(γ([0, 1])) ⊂ V . Let η: [0, 1] → X˜ be the path in X˜ defined such that η(t) = s(f(γ(t))) for all t ∈ [0, 1]. Then η([0, 1]) ⊂ V˜ , and η is the unique path in X˜ for which η(0) = g(z) and p◦η = f ◦γ. But the composition function g ◦γ is a path in X˜, g(γ(0)) = g(z) and p◦g ◦γ = f ◦γ.

Therefore g ◦ γ = η. It follows that g(γ([0, 1])) ⊂ V˜ , and therefore g(z΄) ∈ V˜ .

This proves that g(N_z) ⊂ V˜ . Moreover g(z΄) = s(f(z΄)) for all z΄∈ N_z, and therefore the restriction g|N_z: N_z → X˜ of the function g to the open set N_z is continuous.

We have now shown that, given any point z of Z, there exists an open set N_z in Z such that z ∈ N_z and the restriction g|N_z of g:Z → X˜ to N_z is continuous. It follows from this that the function g is continuous on Z.

Indeed let U be an open set in X˜. Then g⁻¹(U) ∩ N_z is an open set for all z ∈ Z, since g|N_z is continuous. Moreover g⁻¹ (U) is the union of the open sets g⁻¹(U) ∩ N_z as z ranges over all points of Z. It follows that g⁻¹  (U) is itself an open set in Z. Thus g:Z → X˜ is continuous, as required.

Theorem1.19 Let p: X˜ → X be a covering map over a topological space X, and let f:Z → X be a continuous map from some topological space Z into X. Suppose that the topological space Z is both connected and locally path-connected. Suppose also that

                         f_# (π₁(Z, z₀)) ⊂ p_#(π₁(X˜, x˜₀)),

where z₀ and x˜₀ are points of Z and X˜ respectively which satisfy f(z₀) = p(x˜₀). Then there exists a unique continuous map f˜:Z → X˜ for which f˜ (z₀) = x˜₀ and p ◦f˜ = f.

Proof Let P denote the set of all ordered pairs (α, ρ), where α: [0, 1] → Z is a path in Z with α(0) = z₀, ρ: [0, 1] → X˜ is a path in X˜ with ρ(0) = x˜₀,  and f ◦ α = p ◦ ρ. We claim that there is a well-defined function f˜:Z → X˜ characterized by the property that f˜ (α(1)) = ρ(1) for all (α, ρ) ∈ P.

The topological space Z is path-connected, by Proposition 1.14. Therefore, given any point z of Z, there exists a path α in Z from z₀ to z. Moreover it follows from the Path Lifting Theorem that, given any path α in Z from z₀ to z there exists a unique path ρ in X˜ for which ρ(0) = x ˜₀ and p ◦ ρ = f ◦α. It follows that, given any element z of Z, there exists some element (α, ρ) of P for which α(1) = z.

Let (α, ρ) and (β, σ) be elements of P. Suppose that α(1) = β(1). Then  [(f ◦α).(f ◦ β)⁻¹] = f_#[α.β⁻¹]. But f_#(π₁(Z, z₀)) ⊂ p_#(π₁(X˜, x˜₀). Therefore  [(f ◦ α).(f ◦ β)⁻¹] ∈ p_#(π₁(X˜, x˜₀)). It follows from Corollary 1.5 that ρ(1) =σ(1). We conclude therefore that if (α, ρ) and (β, σ) are elements of P, and if α(1) = β(1), then ρ(1) = σ(1). This establishes the existence of a unique function f˜:Z → X˜ characterized by the property that f˜ (α(1)) = ρ(1) for all  (α, ρ) ∈ P. Now p(ρ(1)) = f(α(1)) for all (α, ρ) ∈ P, and therefore p◦f˜ = f.

Also f˜(z₀) = ˜x0, since (ε_z0, ε_x˜0 ) ∈ P, where ε_z0 denotes the constant path in Z based at z0 and ε_x˜0 denotes the constant path in X˜ based at x˜₀. Thus it only remains to show that the map f˜:Z → X˜ is continuous. In view of Lemma 1.18, it suffices to show that f˜ maps paths in Z to paths in X˜.

Let γ: [0, 1] → Z be a path in Z. We claim that the composition function f˜◦ γ is continuous, and is thus a path in X˜. Let α be a path in Z from z₀ to γ(0), let ρ: [0, 1] → X˜ be the unique path in X˜ satisfying ρ(0) = x˜₀ and p ◦ ρ = f ◦ α, and let σ: [0, 1] → X˜ be the unique path in X˜ satisfying σ(0) = ρ(1) and p ◦ σ = f ◦ γ. Now, for each τ ∈ [0, 1], there is a path α_τ : [0, 1] → Z from z0 to γ(τ ) defined such that

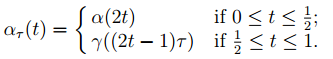
Then f ◦ α_τ (t) = p ◦ ρ_τ (t) for all t ∈ [0, 1] where ρ_τ : [0, 1] → X˜ is the path in X˜ from x˜₀ to σ(τ ) defined such that

It follows that (α_τ , ρ_τ ) ∈ P, for all τ ∈ [0, 1], and therefore f˜ (γ(τ )) = f˜ (α_τ (1)) = ρ_τ (1) = σ(τ )  for all τ ∈ [0, 1]. Thus f˜ ◦ γ = σ. We conclude that f˜◦ γ is a path in X˜ for any path γ in Z. It then follows from Lemma 1.18 that the function f˜:Z → X˜ is a continuous map from Z to X˜ with the required properties.

Corollary 1.20 Let p: X˜ → X be a covering map over a topological space X,  and let f:Z → X be a continuous map from some topological space Z into X.

Suppose that the covering space X˜ is path-connected and that the topological space Z is both connected and locally path-connected. Let z₀ and w₀ be points of Z and X˜ respectively for which f(z₀) = p(w₀). Then there exists a map f˜:Z → X˜ satisfying p ◦ f˜ = f if and only if there exists a subgroup H of π₁(X, p(w₀)) such that H is conjugate to p_#(π₁(X, w˜₀)) and f_#(π₁(Z, z₀)) ⊂ H .

Proof Suppose that there exists a map f˜:Z → X˜ for which p ◦f˜ = f.

Then f_#(π₁(Z, z₀)) ⊂ H, where H = p_#(π₁(X˜,f˜(z₀))). Moreover it follows from Lemma 1.7 that the subgroup H of π₁(X, p(w₀)) is conjugate to p#(π1(X, w˜₀)) in π₁(X, p(w₀)).

Conversely suppose that f_#(π₁(Z, z₀)) ⊂ H, where H is a subgroup of π₁(X, p(w₀)) that is conjugate to p_#(π₁(X, w˜₀)). It follows from Lemma 1.7 that there exists a point x˜ of X˜ for which p(˜x) = p(w0) and p_#(π₁(X ˜, x˜)) = H. Then

                        f_# (π₁(Z, z₀)) ⊂ p_#(π₁(X˜, x˜)).

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد

مواضيع ذات صلة

Triple Torus

Thurston Elliptization Conjecture

Thurston,s Geometrization Conjecture

Real Projective Plane

Pseudometric Topology

Pseudocrosscap

Parallelizable

Möbius Strip

Möbius Shorts

Path

Product Topology

Handle