The term "characteristic" has many different uses in mathematics. In general, it refers to some property that inherently describes a given mathematical object, for example characteristic class, characteristic equation, characteristic factor, etc. However, the unqualified term "characteristic" also has a number of specific meanings depending on context.

For a real number 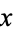,  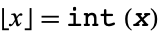is called the characteristic, where  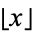is the floor function.

A path in a two-dimensional plane used to transform partial differential equations into systems of ordinary differential equations is also called a characteristic. This form of characteristic was invented by Riemann. For an example of the use of characteristics, consider the equation

Now let 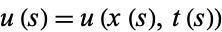. Since

it follows that 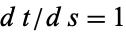, , 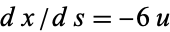and 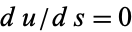. Integrating gives 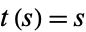, , 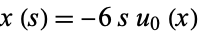and 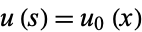, where the constants of integration are 0 and .

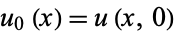REFERENCES:

Farlow, S. J. Partial Differential Equations for Scientists and Engineers. New York: Dover, pp. 205-212, 1993.

Landau, L. D. and Lifschitz, E. M. Fluid Mechanics, 2nd ed. Oxford, England: Pergamon Press, pp. 310-346, 1982.

Moon, P. and Spencer, D. E. Partial Differential Equations. Lexington, MA: Heath, pp. 27-29, 1969.

Whitham, G. B. Linear and Nonlinear Waves. New York: Wiley, pp. 113-142, 1974.

Zauderer, E. Partial Differential Equations of Applied Mathematics, 2nd ed. New York: Wiley, pp. 78-121, 1989.

Zwillinger, D. "Method of Characteristics." §88 in Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, pp. 325-330, 1997.

اخر الاخبار

اخبار العتبة العباسية المقدسة

فرقة العباس تنظم مجلس عزائها السنوي بذكرى شهادة النبي (صلى الله عليه وآله) في النجف

قسم الشؤون الفكرية وجامعة الكوفة يعقدان شراكة علمية لتدريب الطلبة على صيانة المخطوطات وحفظها

بالتزامن مع ذكرى شهادته.. قسم الشؤون الفكرية يصدر كتابًا عن النبي الأعظم (صلى الله عليه وآله)

بالصور.. جموع المؤمنين تحيي ذكرى شهادة الرسول الأكرم عند مرقد الإمام علي (صلوات الله عليهما)

المزيد

الآخبار الصحية

لون أسنانك يتحدث عن صحتك.. إليك ما يقول

عادة يومية بسيطة تخفض الكوليسترول وتحمي القلب

الزنجبيل.. دواء سحري لحماية القلب

المشروبات شديدة السخونة.. "خطر خفي" يهدد صحتك

المزيد

الآخبار التكنلوجية

كيف يمكن لعادات القيادة السيئة أن تؤثر على قيمة سيارتك

في طوفان الذكاء الاصطناعي.. نصائح لحجز "تذكرة النجاة"

هكذا يسرق "قراصنة الذكاء الاصطناعي" المليارات بطرق بسيطة

فيديو لانفجار كرة نارية في سماء اليابان.. ما تفسير ذلك؟

المزيد