Bisection is the division of a given curve, figure, or interval into two equal parts (halves).

A simple bisection procedure for iteratively converging on a solution which is known to lie inside some interval  proceeds by evaluating the function in question at the midpoint of the original interval 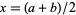 and testing to see in which of the subintervals  or  the solution lies. The procedure is then repeated with the new interval as often as needed to locate the solution to the desired accuracy.

Let 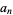 and 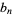 be the endpoints at the 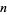th iteration (with  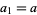and 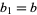) and let  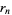be the 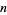th approximate solution. Then the number of iterations required to obtain an error smaller than  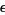is found by noting that

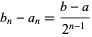(1)

and that 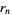 is defined by

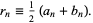(2)

In order for the error to be smaller than ,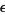

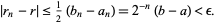(3)

Taking the natural logarithm of both sides then gives

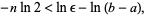(4)

so

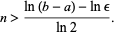(5)

REFERENCES:

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 964-965, 1985.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Bracketing and Bisection." §9.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 343-347, 1992.