The entropy as a state function
Entropy is a state function. To prove this assertion, we need to show that the integral of dS is independent of path. To do so, it is sufficient to prove that the integral of eqn 3.1 around an arbitrary cycle is zero, for that guarantees that the entropy is the same at the initial and final states of the system regardless of the path taken between them (Fig. 3.5). That is, we need to show that
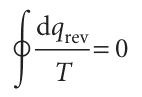
where the symbol denotes integration around a closed path. There are three steps in the argument: 1. First, to show that eqn 3.6 is true for a special cycle (a ‘Carnot cycle’) involving a perfect gas. 2. Then to show that the result is true whatever the working substance. 3. Finally, to show that the result is true for any cycle. A Carnot cycle, which is named after the French engineer Sadi Carnot, consists of four reversible stages (Fig. 3.6): 1. Reversible isothermal expansion from A to B at Th; the entropy change is qh/Th, where qh is the energy supplied to the system as heat from the hot source. 2. Reversible adiabatic expansion from B to C. No energy leaves the system as heat, so the change in entropy is zero. In the course of this expansion, the temperature falls from Th to Tc, the temperature of the cold sink. 3. Reversible isothermal compression from C to D at Tc. Energy is released as heat to the cold sink; the change in entropy of the system is qc/Tc; in this expression qc is negative. 4. Reversible adiabatic compression from D to A. No energy enters the system as heat, so the change in entropy is zero. The temperature rises from Tc to Th. The total change in entropy around the cycle is
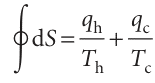
However, we show in Justification 3.1 that, for a perfect gas:
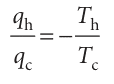
Substitution of this relation into the preceding equation gives zero on the right, which is what we wanted to prove.
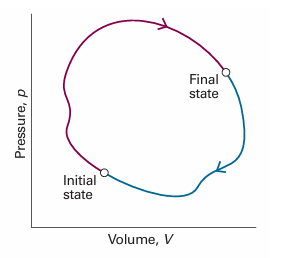
Fig. 3.5 In a thermodynamic cycle, the overall change in a state function (from the initial state to the final state and then back to the initial state again) is zero.
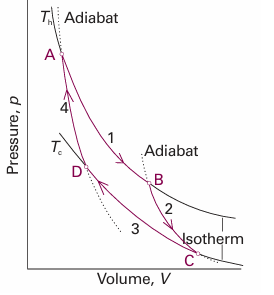
Fig. 3.6 The basic structure of a Carnot cycle. In Step 1, there is isothermal reversible expansion at the temperature Th. Step 2 is a reversible adiabatic expansion in which the temperature falls from Th to Tc. In Step 3 there is an isothermal reversible compression at Tc, and that isothermal step is followed by an adiabatic reversible compression, which restores the system to its initial state.
In the second step we need to show that eqn 3.7 applies to any material, not just a perfect gas (which is why, in anticipation, we have not labelled it with a °). We begin this step of the argument by introducing the efficiency, ε (epsilon), of a heat engine:
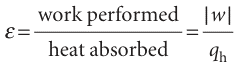
The definition implies that, the greater the work output for a given supply of heat from the hot reservoir, the greater is the efficiency of the engine. We can express the definition in terms of the heat transactions alone, because (as shown in Fig. 3.7) the energy supplied as work by the engine is the difference between the energy supplied as heat by the hot reservoir and returned to the cold reservoir:
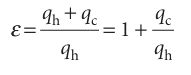
(Remember that qc< 0.) It then follows from eqn 3.7 that
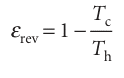
Now we are ready to generalize this conclusion. The Second Law of thermodynamics implies that all reversible engines have the same efficiency regardless of their construction. To see the truth of this statement, suppose two reversible engines are coupled together and run between the same two reservoirs (Fig. 3.8). The working substances and details of construction of the two engines are entirely arbitrary. Initially, suppose that
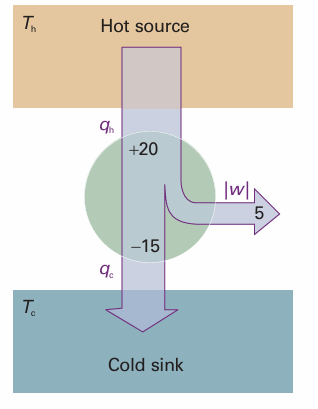
Fig. 3.7 Suppose an energy qh (for example, 20 kJ) is supplied to the engine and qc is lost from the engine (for example, qc =−15 kJ) and discarded into the cold reservoir. The work done by the engine is equal to qh + qc (for example, 20 kJ + (−15 kJ) = 5 kJ). The efficiency is the work done divided by the energy supplied as heat from the hot source.
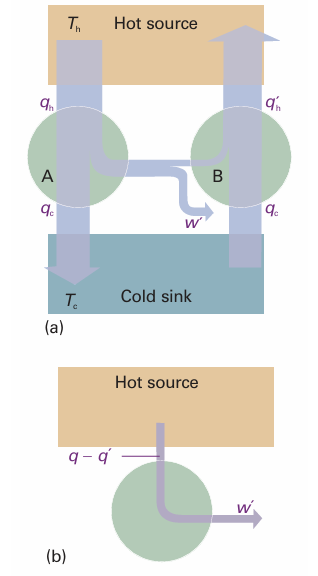
Fig. 3.8 (a) The demonstration of the equivalence of the efficiencies of all reversible engines working between the same thermal reservoirs is based on the f low of energy represented in this diagram. (b) The net effect of the processes is the conversion of heat into work without there being a need for a cold sink: this is contrary to the Kelvin statement of the Second Law.
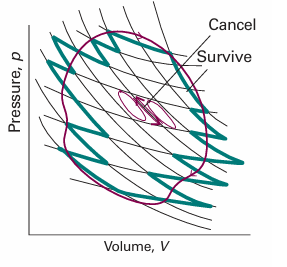
Fig. 3.9 A general cycle can be divided into small Carnot cycles. The match is exact in the limit of infinitesimally small cycles. Paths cancel in the interior of the collection, and only the perimeter, an increasingly good approximation to the true cycle as the number of cycles increases, survives. Because the entropy change around every individual cycle is zero, the integral of the entropy around the perimeter is zero too.
engine A is more efficient than engine B and that we choose a setting of the controls that causes engine B to acquire energy as heat qc from the cold reservoir and to release a certain quantity of energy as heat into the hot reservoir. However, because engine A is more efficient than engine B, not all the work that A produces is needed for this pro cess, and the difference can be used to do work. The net result is that the cold reservoir is unchanged, work has been done, and the hot reservoir has lost a certain amount of energy. This outcome is contrary to the Kelvin statement of the Second Law, because some heat has been converted directly into work. In molecular terms, the random thermal motion of the hot reservoir has been converted into ordered motion characteristic of work. Because the conclusion is contrary to experience, the initial assumption that engines A and B can have different efficiencies must be false. It follows that the relation between the heat transfers and the temperatures must also be independent of the working material, and therefore that eqn 3.7 is always true for any substance involved in a Carnot cycle. For the final step in the argument, we note that any reversible cycle can be approximated as a collection of Carnot cycles and the cyclic integral around an arbitrary path is the sum of the integrals around each of the Carnot cycles (Fig. 3.9). This approximation becomes exact as the individual cycles are allowed to become infinitesimal. The entropy change around each individual cycle is zero (as demonstrated above), so the sum of entropy changes for all the cycles is zero. However, in the sum, the entropy change along any individual path is cancelled by the entropy change along the path it shares with the neighbouring cycle. Therefore, all the entropy changes cancel except for those along the perimeter of the overall cycle. That is,
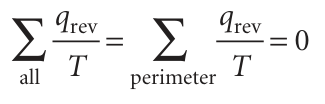
In the limit of infinitesimal cycles, the non-cancelling edges of the Carnot cycles match the overall cycle exactly, and the sum becomes an integral. Equation 3.6 then follows immediately. This result implies that dS is an exact differential and therefore that S is a state function.
The discussion of the text is the basis of the thermodynamic assessment of the power needed to cool objects in refrigerators. First, we consider the work required to cool an object, and refer to Fig. 3.10. When an energy |qc| is removed from a cool source at a temperature Tc and then deposited in a warmer sink at a temperature Th, as in a typical refrigerator, the change in entropy is
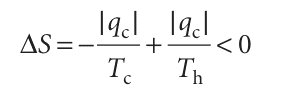
The process is not spontaneous because not enough entropy is generated in the warm sink to overcome the entropy loss from the hot source. To generate more entropy, energy must be added to the stream that enters the warm sink. Our task is to find the minimum energy that needs to be supplied. The outcome is expressed as the coefficient of performance, c:
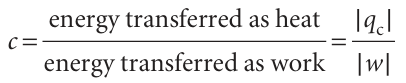
The less the work that is required to achieve a given transfer, the greater the coefficient of performance and the more efficient the refrigerator.
Because |qc| is removed from the cold source, and the work |w| is added to the energy stream, the energy deposited as heat in the hot sink is |qh|=|qc|+|w|. Therefore,
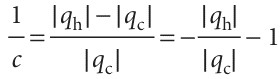
We can now use eqn 3.7 to express this result in terms of the temperatures alone, which is possible if the transfer is performed reversibly. This substitution leads to
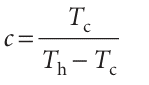
for the thermodynamically optimum coefficient of performance. For a refrigerator withdrawing heat from ice-cold water (Tc = 273 K) in a typical environment (Th = 293 K), c = 14, so, to remove 10 kJ (enough to freeze 30 g of water), requires transfer of at least 0.71 kJ as work. Practical refrigerators, of course, have a lower coefficient of performance. The work to maintain a low temperature is also relevant to the design of refrigerators. No thermal insulation is perfect, so there is always a flow of energy as heat into the sample at a rate proportional to the temperature difference. If the rate at which energy leaks in is written A(Th − Tc), where A is a constant that depends on the size of the sample and the details of the insulation, then the minimum power, P, required to maintain the original temperature difference by pumping out that energy by heating the surroundings is
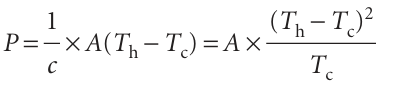
We see that the power increases as the square of the temperature difference we are trying to maintain. For this reason, air-conditioners are much more expensive to run on hot days than on mild days.
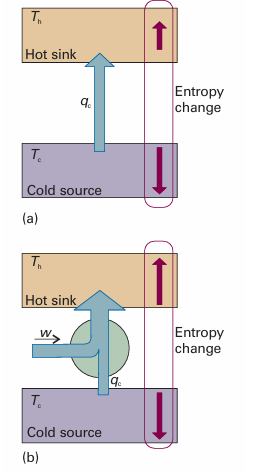
Fig. 3.10 (a) The flow of energy as heat from a cold source to a hot sink is not spontaneous. As shown here, the entropy increase of the hot sink is smaller than the entropy increase of the cold source, so there is a net decrease in entropy. (b) The process becomes feasible if work is provided to add to the energy stream. Then the increase in entropy of the hot sink can be made to cancel the entropy decrease of the hot source.
 الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


