

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Introduction to Algebra
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
www.almerja.com
الجزء والصفحة:
...
6-3-2017
1347
Algebra sounds like a difficult concept, and you may have heard that it is from an older sibling or parent. Don't worry-- it's not hard at all. The basic idea is that we have an equation that is balanced on both sides. Picture a scale in your head with the same values on each side, and you have a basic understanding of algebra.

Notice how there is a six on each side, and so they are equal and the scale is balanced? That is your first equation! You've probably realized too that we can perform operations on each side of the equation (scale). Writing 4+2 on one side and 3+3 on the other will keep the scale balanced, right?

Of course, you don't have to use addition. Any of the other arithmetic operations, like subtraction, multiplication, or division will work, so long as each side is equal to the other. We will now convert the picture of the scale into an equation. This is a simple process, and all you have to do is place your two values on opposite sides of an equals sign.
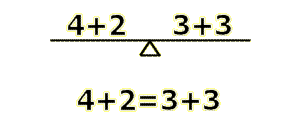
That's a great equation we have created, but it serves no purpose. It is obvious to anyone that 4+2=3+3, because 6=6. The equation is useful in finding the value of a missing number. Say we had a equation like this:
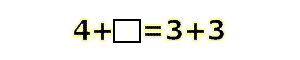
The empty box indicates a missing number. We know something should go there, but what? This equation can be solved by adding 3+3 to get 6, and then recognizing that 4+2=6. The number 2 is the missing number. Now we have actually accomplished something with our new friend, the equation.
The next step in algebra is learning about a variable. Variables are defined as numbers that can change value or represent a missing value. The empty box in our last equation was a variable, but drawing cute little shapes can get tiresome. Variables are usually represented by letters of the alphabet, and for whatever reason x, y, and z are the most commonly used variables. Here's how our last equation would look using a variable:
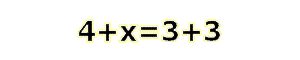
Notice that the 'x' is a variable, NOT the multiplication sign. It is customary in math to use the * sign to represent multiplication so that variables don't get confused with operations. Our goal in the equation is to solve for the variable x, and you might be able to do so using trial and error, but there is an easier way. Since we have a balanced equation, we can do anything to one side, but we have to do the same to the other side. For instance, we can add 1 to each side, resulting in 4+x+1=3+3+1. Adding 1 to only one side would create an inequality, which is not what we want.
The best way to solve is by isolating the variable on one side of the equation, so that we can tell what value it holds by looking at the other side of the equation, as in x=4. To do this, we must get rid of the 4. Since we can do anything to both sides of the equation, why not subtract 4 from each side?

On the left side of the equation, 4-4 is obviously 0, so we can get rid of that, and 3+3=6, minus 4 is 2, so we can write 2 in place of 3+3-4.

Remember- the goal is to get the variable alone by doing the same thing to each side. In an equation like 4x + 4 = 12, you would subtract 4 from each side to get 4x = 8. Divide each side by four and you've got x=2. Now you've got a basic understanding of algebra, and can solve equations like 7+x=14. If not,
 الاكثر قراءة في مواضيع عامة في الجبر
الاكثر قراءة في مواضيع عامة في الجبر
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)


















