

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Matrix Multiplication
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
www.almerja.com
الجزء والصفحة:
...
6-3-2017
6522
You probably know what a matrix is already if you are interested in matrix multiplication. However, a quick example won't hurt. A matrix is just a two-dimensional group of numbers. Instead of a list, called a vector, a matrix is a rectangle, like the following:
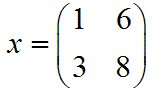
You can set a variable to be a matrix just as you can set a variable to be a number. In this case, x is the matrix containing those four numbers (in that particular order). Now, suppose you have two matrices that you need to multiply. Multiplication for numbers is pretty easy, but how do you do it for a matrix?
Here is a key point: You cannot just multiply each number by the corresponding number in the other matrix. Matrix multiplication is not like addition or subtraction. It is more complicated, but the overall process is not hard to learn. Here's an example first, and then I'll explain what I did:
Example:

Solution:
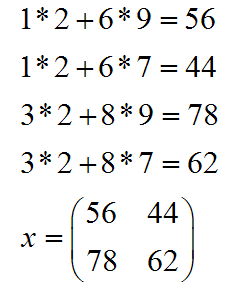
You're probably wondering how in the world I got that answer. Well you're justified in thinking that. Matrix multiplication is not an easy task to learn, and you do need to pay attention to avoid a careless error or two. Here's the process:
- Step 1: Move across the top row of the first matrix, and down the first column of the second matrix:

- Step 2: Multiply each number from the top row of the first matrix by the number in the first column on the second matrix. In this case, that means multiplying 1*2 and 6*9. Then, take the sum of those values (2+54):
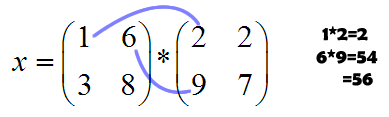
- Step 3: Insert the value you just got into the answer matrix. Since we are multiplying the 1st row and the 1st column, our answer goes into that slot in the answer matrix:
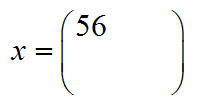
- Step 4: Repeat for the other rows and columns. That means you need to walk down the first row of the first matrix and this time the second column of the second matrix. Then the second row of the first matrix and the first column of the second, and finally the bottom of the first matrix and the right column of the second matrix:

- Step 5: Insert all of those values into the answer matrix. I just showed you how to do top left and the bottom right. If you work the other two numbers, you will get 1*2+6*7=44 and 3*2+8*9=78. Insert them into the answer matrix in the corresponding positions and you get:
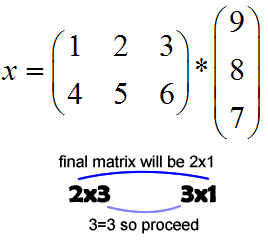
Now I know what you're thinking. That was really hard!!! Well it will seem that way until you get used to the process. It may help you to write out all your work, and even draw arrows to remember which way you're moving in the rows and columns. Just remember to multiply each row in the first matrix by each column in the second matrix.
What if the matrices aren't squares? Then you have to add another step. In order to multiply two matrices, the matrix on the left must have as many columns as the matrix on the right has rows. That way you can match up each pair while you're multiplying. The size of the final matrix is determined by the rows in the left matrix and the columns in the right. Here's what I do:
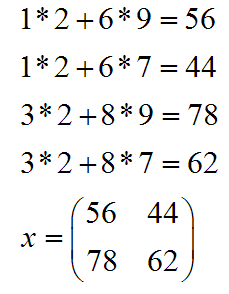
I write down the sizes of the matrices. The left matrix has 2 rows and 3 columns, so that's how we write it. Rows, columns, in that order. The other matrix is a 3x1 matrix because it has 3 rows and just 1 column. If the numbers in the middle match up you can multiply. The outside numbers give you the size of the answer. Even if you mess this up you'll figure it out eventually because you won't be able to multiply.
Here's an important reminder: Matrix Multiplication is not commutative. That means you cannot switch the order and expect the same result! Regular multiplication tells us that 4*3=3*4, but this is not multiplication of the usual sense.
Finally, here's an example with uneven matrix sizes to wrap things up:
Example:
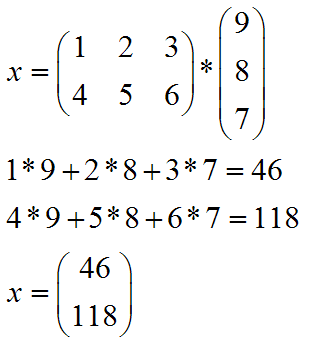
 الاكثر قراءة في مواضيع عامة في الجبر
الاكثر قراءة في مواضيع عامة في الجبر
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















