

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Angles-Degrees (Angles)
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
www.almerja.com
الجزء والصفحة:
...
12-3-2017
2006
|
|
We can measure Angles in Degrees. There are 360 degrees in one Full Rotation (one (Angles can also be measured in Radians) |
(Note: "Degrees" can also mean Temperature, but here we are talking about Angles)
The Degree Symbol: °
We use a little circle ° following the number to mean degrees.
For example 90° means 90 degrees
One Degree

This is how large 1 Degree is
|
The Full Circle A Full Circle is 360° Half a circle is 180° Quarter of a circle is 90° |
|
|
|
|
Why 360 degrees? Probably because old calendars (such as the Persian Calendar) used 360 days for a year - when they watched the stars they saw them revolve around the North Star one degree per day. Also 360 can be divided evenly by 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120 and 180, which makes a lot of basic geometry easier. |
Measuring Degrees
We often measure degrees using a protractor:
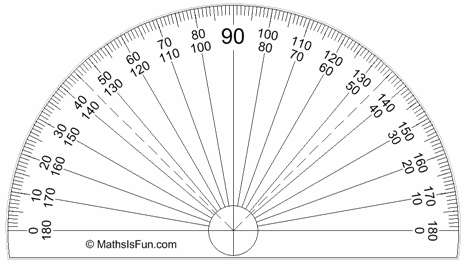
The normal protractor measures 0° to 180°
|
|
There are also full-circle protractors. But they are not as commonly used because they are a bit big and don't do anything special. |
Radians
|
|
|
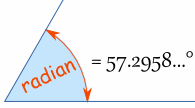
We can measure Angles in Radians. 1 Radian is about 57.2958 degrees. |
Does 57.2958... degrees seem a strange value?
Maybe degrees are strange, as the Radian is a pure measure based on the Radius of the circle:
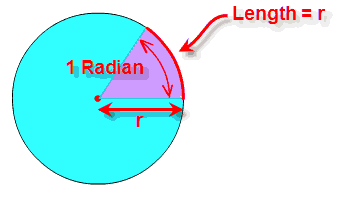
Radian: the angle made by taking the radius
and wrapping it along the edge of a circle:
|
So, a Radian "cuts out" a length of a circle's circumference equal to the radius. |
|
Radians and Degrees

So:
- There are π radians in a half circle
- And also 180° in a half circle
So π radians = 180°
So 1 radian = 180°/π = 57.2958° (approximately)
|
Degrees |
Radians |
Radians |
|
30° |
π/6 |
0.524 |
|
45° |
π/4 |
0.785 |
|
60° |
π/3 |
1.047 |
|
90° |
π/2 |
1.571 |
|
180° |
π |
3.142 |
|
270° |
3π/2 |
4.712 |
|
360° |
2π |
6.283 |
Example: How Many Radians in a Full Circle?
Imagine you cut up pieces of string exactly the length from thecenter of a circle to its edge ...
... how many pieces would you need to go around the edge of the circle?
Answer: 2π (or about 6.283 pieces of string). 
Radians Preferred by Mathematicians
Because the radian is based on the pure idea of "the radius being laid along the circumference", it often gives simple and natural results when used in mathematics.
For example, look at the sine function for very small values:
|
x (radians) |
1 |
0.1 |
0.01 |
0.001 |
|
sin(x) |
0.8414710 |
0.0998334 |
0.0099998 |
0.0009999998 |
For very small values. "x" and "sin(x)" are almost the same
(as long as "x" is in Radians!)
There will be other examples like that as you learn more about mathematics.
Conclusion
So, degrees are easier to use in everyday work, but radians are much better for mathematics.
Congruent Angles
Congruent Angles have the same angle (in degrees or radians). That is all.
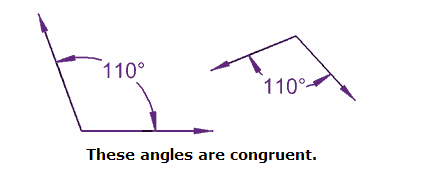
These angles are congruent.
They don't have to point in the same direction.
They don't have to be on similar sized lines.
Just the same angle.
Congruent - why such a funny word that basically means "equal"? Probably because they would only be "equal" if laid on top of each other. Anyway it comes from Latin congruere, "to agree". So the angles "agree"
Parallel Lines, and Pairs of Angles
Parallel Lines
Lines are parallel if they are always the same distance apart (called "equidistant"), and will never meet. Just remember:
Always the same distance apart and never touching.
The red line is parallel to the blue line in both these cases:
|
|
|
|
|
Example 1 |
Example 2 |
Parallel lines also point in the same direction.
|
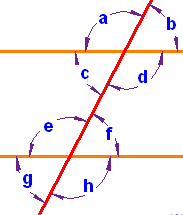
Pairs of Angles When parallel lines get crossed by another line (which is called aTransversal), you can see that many angles are the same, as in this example: These angles can be made into pairs of angles which have special names.
|
|
Testing for Parallel Lines
Some of those special pairs of angles can be used to test if lines really are parallel:
|
|
|
Examples
|
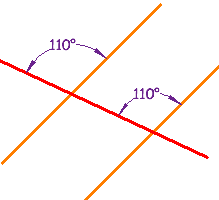
These lines are parallel, because a pair ofCorresponding Angles are equal. |
|
|
|
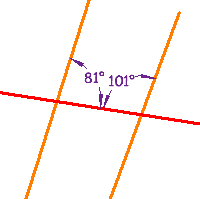
These lines are not parallel, because a pair ofConsecutive Interior Anglesdo not add up to 180° (81° + 101° =182°) |
|
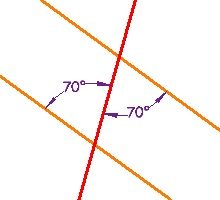
These lines are parallel, because a pair of Alternate Interior Angles are equal |
|
Transversals
A Transversal is a line that crosses at least two other lines.
The red line is the transversal in each example:
|
|
||
|
Transversal crossing two lines |
this Transversal crosses twoparallel lines |
... and this one cuts across three lines |
Triangles Contain 180°
|
|
In a triangle, the three angles always add to 180°: A + B + C = 180° |
Try it yourself (drag the points):
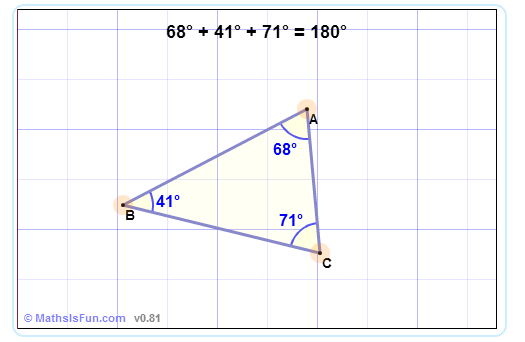
We can use that fact to find a missing angle in a triangle:
Example: Find the Missing Angle "C"
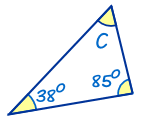
|
Start With: |
|
A + B + C = 180° |
|
|
|
|
|
Fill in what we know: |
|
38° + 85° + C = 180° |
|
|
|
|
|
Rearrange |
|
C = 180° - 38° - 85° |
|
|
|
|
|
Calculate: |
|
C = 57° |
Proof
This is a proof that the angles in a triangle equal 180°:
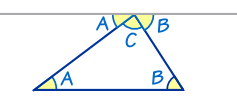
The top line (that touches the top of the triangle) is
running parallel to the base of the triangle.
So:
- angles A are the same
- angles B are the same
And you can easily see that A + C + B does a complete rotation from one side of the straight line to the other, or 180°
Supplementary Angles
Two Angles are Supplementary if they add up to 180 degrees.
|
These two angles (140° and 40°) are Supplementary Angles, because they add up to 180°. Notice that together they make astraight angle. |
|
|
|
|
|
But the angles don't have to be together. These two are supplementary because 60° + 120° = 180° |
|
Complementary Angles
Two angles are Complementary when they
add up to 90 degrees (a Right Angle 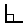 ).
).
|
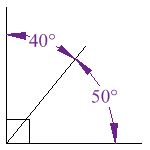
These two angles (40° and 50°) are Notice that together they make a right angle |
|
|
|
|
|
But the angles don't have to be together. These two are complementary because 27° + 63° = 90° |
|

|
Right Angled Triangle In a right angled triangle, the two non-right angles are complementary, because in a triangle the three angles add to 180°, and 90° has already been taken by the right angle. |
|
 الاكثر قراءة في الهندسة المستوية
الاكثر قراءة في الهندسة المستوية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية
























 .
.



 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















