

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
The Circle
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
www.almerja.com
الجزء والصفحة:
...
14-3-2017
3052
Circle
|
|
A circle is easy to make: Draw a curve that is "radius" away And so: All points are the same distance from the center. |
|
You Can Draw It Yourself Put a pin in a board, put a loop of string around it, and insert a pencil into the loop. Keep the string stretched and draw the circle! |
|
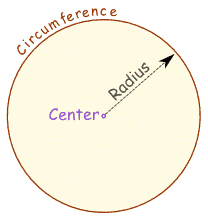
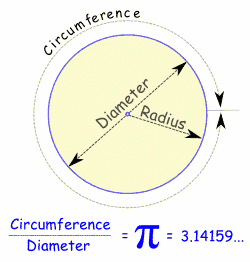
Radius, Diameter and Circumference
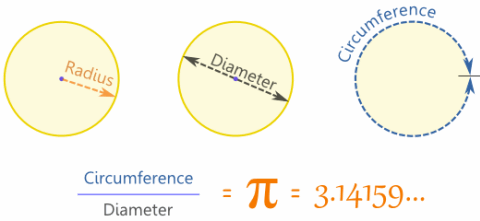
The Radius is the distance from the center to the edge.
The Diameter starts at one side of the circle, goes through the center and ends on the other side.
The Circumference is the distance around the edge of the circle.
And here is the really cool thing:
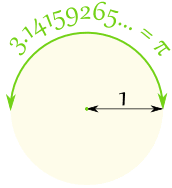
When you divide the circumference by the diameter you get 3.141592654...
which is the number π (Pi)
|
So when the diameter is 1, the circumference is 3.141592654... |
|
|
We can say:
Circumference = π × Diameter
Example: You walk around a circle which has a diameter of 100m, how far have you walked?
|
|
Distance walked = Circumference = π × 100m = 314m (to the nearest m) |
Also note that the Diameter is twice the Radius:
Diameter = 2 × Radius
And so this is also true:
Circumference = 2 × π × Radius
Remembering
The length of the words may help you remember:
- Radius is the shortest word
- Diameter is longer (and is 2 × Radius)
- Circumference is the longest (and is π × Diameter)
Definition
|
The circle is a plane shape (two dimensional): And the definition of a circle is: |
|
|
The set of all points on a plane that are a fixed distance from a center.
Area

The area of a circle is π times the radius squared, which is written:
A = π r2
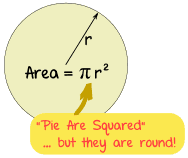
To help you remember think "Pie Are Squared"
(even though pies are usually round)
Or, in relation to Diameter:
A = (π/4) × D2
Example: What is the area of a circle with radius of 1.2 m ?
A = π × r2
A = π × 1.22
A = π × (1.2 × 1.2)
A = 3.14159... × 1.44 = 4.52 (to 2 decimals)
Area Compared to a Square
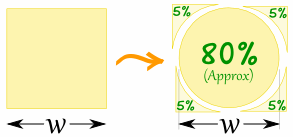
A circle has about 80% of the area of a similar-width square.
The actual value is (π/4) = 0.785398... = 78.5398...%
Names
Because people have studied circles for thousands of years special names have come about.
Nobody wants to say "that line that starts at one side of the circle, goes through the center and ends on the other side" when a word like "Diameter" would do.
So here are the most common special names:
|
|
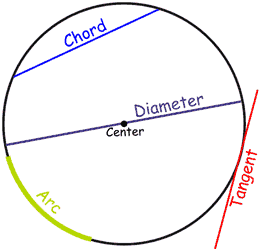
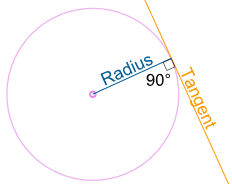
Lines A line that goes from one point to another on the circle's circumference is called a Chord. If that line passes through the center it is called aDiameter. A line that "just touches" the circle as it passes by is called a Tangent. And a part of the circumference is called an Arc. |
|
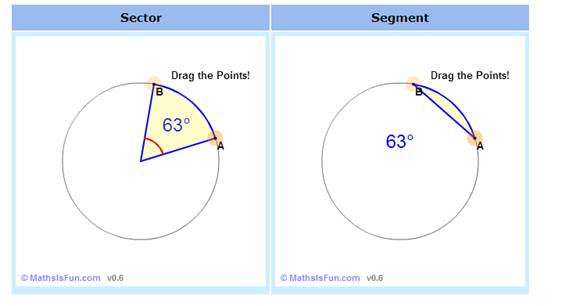
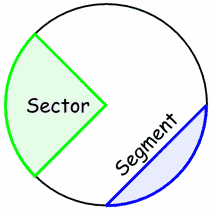
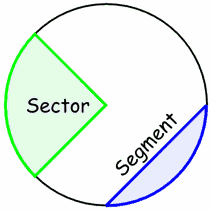
Slices There are two main "slices" of a circle The "pizza" slice is called a Sector. And the slice made by a chord is called a Segment. |
|
Common Sectors
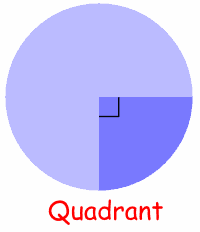
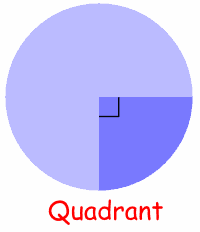
The Quadrant and Semicircle are two special types of Sector:
|
|
Quarter of a circle is called a Quadrant. |
|
|
Inside and Outside
|
|
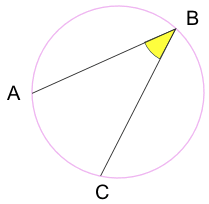
A circle has an inside and an outside (of course!). But it also has an "on", because you could be right on the circle. Example: "A" is outside the circle, "B" is inside the circle and "C" is on the circle. |
Pi (π)
|
|
|
Draw a circle with a radius of 1. The distance half way around the edge of the circle |
|
Or you could draw a circle with a diameter of 1. Then the circumference (the distance all the way |
|
|
|
|
|
Pi (the symbol is the Greek letter π) is: The ratio of the Circumference |
|
In other words, if you measure the circumference, and then divide by the diameter of the circle you get the number π It is approximately equal to: 3.14159265358979323846… The digits go on and on with no pattern. In fact, π has been calculated to over two quadrillion decimal places and still there is no pattern. |
|
Example: You walk around a circle which has a diameter of 100m, how far have you walked?
|
|
Distance walked = Circumference = π × 100m = 314.159...m = 314m (to the nearest m) |
Approximation
A quick and easy approximation for π is 22/7
22/7 = 3.1428571...
But as you can see, 22/7 is not exactly right. In fact π is not equal to the ratio of any two numbers, which makes it an irrational number.
A better approximation (but stll not exact) is:
355/113 = 3.1415929...
(think "113355", then divide the "355" by the "113")
Remembering
I usually just remember "3.14159", but you can also count the letters of:
"May I have a large container of butter today"
3 1 4 1 5 9 2 6 5
To 100 Decimal Places
Here is π with the first 100 decimal places:
|
3.14159265358979323846264338327950288419716939937510 58209749445923078164062862089986280348253421170679... |
Circle Sector and Segment
|
Slices There are two main "slices" of a circle:
|
|
Common Sectors
The Quadrant and Semicircle are two special types of Sector:
|
|
Quarter of a circle is called a Quadrant. |
|
|
|
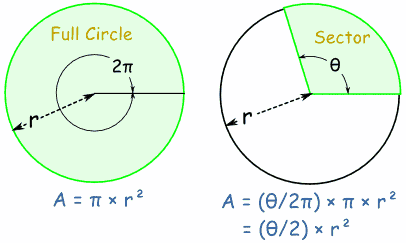
Area of a Sector You can work out the Area of a Sector by comparing its angle to the angle of a full circle. Note: I am using radians for the angles. |
|
|
This is the reasoning:
Area of Sector = ½ × θ × r2 (when θ is in radians) Area of Sector = ½ × (θ × π/180) × r2 (when θ is in degrees) |
|
|
|
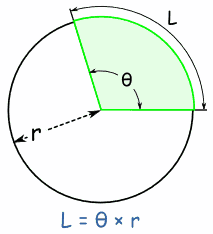
Arc Length By the same reasoning, the arc length (of a Sector or Segment) is: L = θ × r (when θ is in radians) L = (θ × π/180) × r (when θ is in degrees) |
|
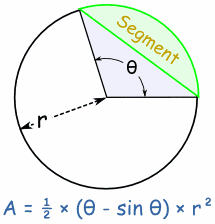
Area of Segment The Area of a Segment is the area of a sector minus the triangular piece (shown in light blue here). There is a lengthy reason, but the result is a slight modification of the Sector formula: |
|
|||||||||||||||||||||||
|
Area of Segment = ½ × (θ - sin θ) × r2 (when θ is in radians) Area of Segment = ½ × ( (θ × π/180) - sin θ) × r2 (when θ is in degrees) Area of a Circle by Cutting into Sectors
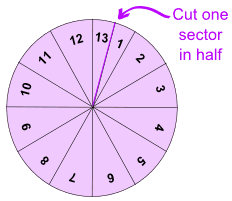
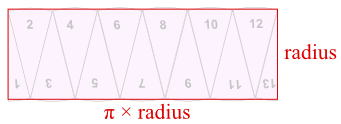
Here is a way to find the formula for the area of a circle:
Cut a circle into equal sectors (12 in this example) Divide just one of the sectors into two equal parts. You now have thirteen sectors – number them 1 to 13:
Rearrange the 13 sectors like this:
Which resembles a rectangle:
What are the (approximate) height and width of the rectangle? The height is the circle's radius: just look at sectors 1 and 13 above. When they were in the circle they were "radius" high. The width (actually one "bumpy" edge) is half of the curved parts along the circle's edge ... in other words it is about half the circumference of the circle. We know that: Circumference = 2 × π × radius And so the width is about: Half the Circumference = π × radius And so we have (approximately):
Now we just multply the width by the height to find the area of the rectangle: Area = (π × radius) × (radius) = π × radius2 Note: The rectangle and the "bumpy edged shape" made by the sectors are not an exact match. But we could get a better result if we divided the circle into 25 sectors (23 with an angle of 15° and 2 with an angle of 7.5°). And the more we divided the circle up, the closer we would get to being exactly right. Conclusion Area of Circle = π r2 Annulus
Area Because it is a circle with a circular hole, you can calculate the area by subtracting the area of the "hole" from the big circle's area:
Area = πR2 - πr2
Example: a steel pipe has an outside diameter (OD) of 100mm and an inside diameter (ID) of 80mm, what is the area of the cross section? Convert diameter to radius for both outside and inside circles:
Now calculate area: Area = π( R2 - r2 ) Area = 3.14159... × ( 502 - 402 ) Area = 3.14159... × ( 2500 - 1600 ) Area = 3.14159... × 900 Area = 2827 mm2 (to nearest mm2) Circle Theorems Some interesting things about angles and circles. Inscribed Angle First off, a definition: Inscribed Angle: an angle made from points sitting on the circle's circumference.
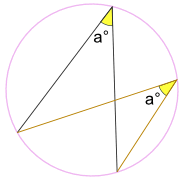
Inscribed Angle Theorems An inscibed angle a° is half of the central angle 2a°
And (keeping the endpoints fixed) ... ... the angle a° is always the same, no matter where it is on the circumference:
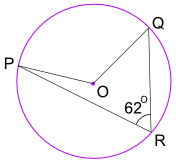
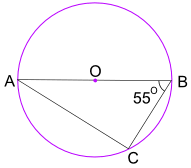
Example: What is the size of Angle POQ? (O is circle's center)
Example: What is the size of Angle CBX?
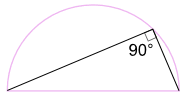
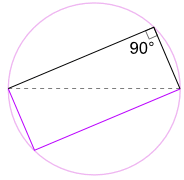
Angle in a Semicircle An angle inscribed in a semicircle is always a right angle:
Example: What is the size of Angle BAC?
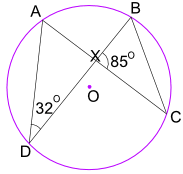
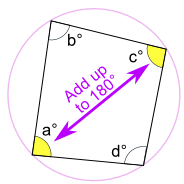
Cyclic Quadrilateral
Example: What is the size of Angle WXY?
|
||||||||||||||||||||||||
 الاكثر قراءة في الهندسة المستوية
الاكثر قراءة في الهندسة المستوية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية




























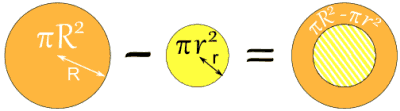







 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















