


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-6-2018
Date: 5-7-2018
Date: 22-5-2018
|
The second-order ordinary differential equation
 |
(1) |
sometimes called the hyperspherical differential equation (Iyanaga and Kawada 1980, p. 1480; Zwillinger 1997, p. 123). The solution to this equation is
![y=(x^2-1)^(-mu/2)[C_1P_nu^mu(x)+C_2Q_nu^mu(x)],](http://mathworld.wolfram.com/images/equations/GegenbauerDifferentialEquation/NumberedEquation2.gif) |
(2) |
where 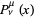 is an associated Legendre function of the first kind and
is an associated Legendre function of the first kind and 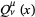 is an associated Legendre function of the second kind.
is an associated Legendre function of the second kind.
A number of other forms of this equation are sometimes also known as the ultraspherical or Gegenbauer differential equation, including
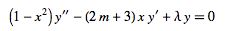 |
(3) |
The general solutions to this equation are
![y=(x^2-1)^((1-2mu)/4)[C_1P_(-1/2+mu+nu)^(1/2-mu)(x)+C_2Q_(-1/2+mu+nu)^(1/2-mu)(x)].](http://mathworld.wolfram.com/images/equations/GegenbauerDifferentialEquation/NumberedEquation4.gif) |
(4) |
If 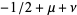 is an integer, then one of the solutions is known as a Gegenbauer polynomials
is an integer, then one of the solutions is known as a Gegenbauer polynomials 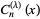 , also known as ultraspherical polynomials.
, also known as ultraspherical polynomials.
The form
 |
(5) |
is also given by Infeld and Hull (1951, pp. 21-68) and Zwillinger (1997, p. 122). It has the solution
![y=(x^2-1)^(-(2m+1)/4)[C_1P_(-1/2+sqrt((1+m)^2+lambda))^(1/2+m)(x)+C_2Q_(-1/2+sqrt((1+m)^2+lambda))^(1/2+m)(x)].](http://mathworld.wolfram.com/images/equations/GegenbauerDifferentialEquation/NumberedEquation6.gif) |
(6) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.
Infeld, L. and Hull, T. E. "The Factorization Method." Rev. Mod. Phys. 23, 21-68, 1951.
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, 1980.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 547-549, 1953.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 127, 1997.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|