


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-12-2018
Date: 12-7-2018
Date: 11-6-2018
|
The ordinary differential equation
![(x^2-b^2)(x^2-c^2)(d^2z)/(dx^2)+x(x^2-b^2+x^2-c^2)(dz)/(dx)-[m(m+1)x^2-(b^2+c^2)p]z=0.](http://mathworld.wolfram.com/images/equations/LamesDifferentialEquation/NumberedEquation1.gif) |
(1) |
(Byerly 1959, p. 255). The solution is denoted 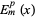 and is known as an ellipsoidal harmonic of the first kind, or Lamé function. Whittaker and Watson (1990, pp. 554-555) give the alternative forms
and is known as an ellipsoidal harmonic of the first kind, or Lamé function. Whittaker and Watson (1990, pp. 554-555) give the alternative forms
![4Delta_lambdad/(dlambda)[Delta_lambda(dLambda)/(dlambda)]=[n(n+1)lambda+C]Lambda](http://mathworld.wolfram.com/images/equations/LamesDifferentialEquation/Inline2.gif) |
(2) |
/(dlambda)](http://mathworld.wolfram.com/images/equations/LamesDifferentialEquation/Inline3.gif) |
(3) |
![=([n(n+1)lambda+C]Lambda)/(4Delta_lambda)](http://mathworld.wolfram.com/images/equations/LamesDifferentialEquation/Inline4.gif) |
(4) |
![(d^2Lambda)/(du^2)=[n(n+1)P(u)+C-1/3n(n+1)(a^2+b^2+c^2)]Lambda](http://mathworld.wolfram.com/images/equations/LamesDifferentialEquation/Inline5.gif) |
(5) |
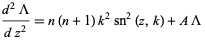 |
(6) |
(Whittaker and Watson 1990, pp. 554-555; Ward 1987; Zwillinger 1997, p. 124). Here, 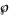 is a Weierstrass elliptic function,
is a Weierstrass elliptic function, 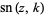 is a Jacobi elliptic function, and
is a Jacobi elliptic function, and
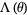 |
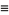 |
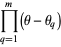 |
(7) |
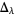 |
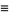 |
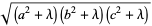 |
(8) |
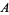 |
 |
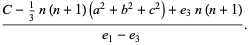 |
(9) |
Two other equations named after Lamé are given by
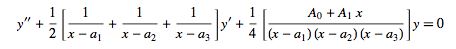 |
(10) |
and
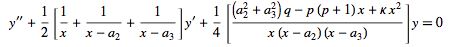 |
(11) |
(Moon and Spencer 1961, p. 157; Zwillinger 1997, p. 124).
REFERENCES:
Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, 1959.
Moon, P. and Spencer, D. E. Field Theory for Engineers. New York: Van Nostrand, 1961.
Ward, R. S. "The Nahm Equations, Finite-Gap Potentials and Lamé Functions." J. Phys. A: Math. Gen. 20, 2679-2683, 1987.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 124, 1997.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|