
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-3-2019
Date: 25-3-2019
Date: 15-10-2019
|
Borwein et al. (2004, pp. 4 and 44) term the expression of the integrals
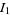 |
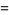 |
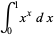 |
(1) |
 |
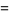 |
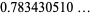 |
(2) |
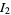 |
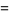 |
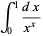 |
(3) |
 |
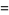 |
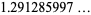 |
(4) |
(OEIS A083648 and A073009) in terms of infinite sums "a sophomore's dream."
For 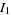 , write
, write
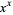 |
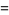 |
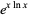 |
(5) |
 |
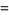 |
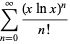 |
(6) |
Integrating term by term then gives
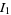 |
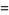 |
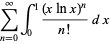 |
(7) |
 |
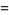 |
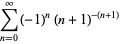 |
(8) |
 |
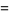 |
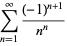 |
(9) |
(Borwein et al. 2004, p. 44).
For 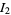 , write
, write
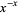 |
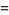 |
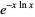 |
(10) |
 |
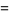 |
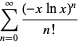 |
(11) |
Integrating term by term then gives
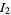 |
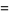 |
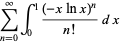 |
(12) |
 |
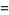 |
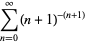 |
(13) |
 |
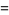 |
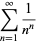 |
(14) |
(Borwein et al. 2004, pp. 4 and 44).
REFERENCES:
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Dunham, W. The Calculus Gallery: Masterpieces from Newton to Lebesgue. Princeton, NJ: Princeton University Press, pp. 46-51, 2005.
Sloane, N. J. A. Sequences A083648 and A073009 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|