Beltrami Identity

An identity in calculus of variations discovered in 1868 by Beltrami. The Euler-Lagrange differential equation is

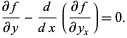(1)

Now, examine the derivative of 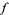 with respect to 

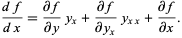(2)

Solving for the 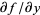 term gives

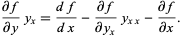(3)

Now, multiplying (1) by 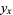 gives

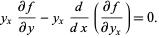(4)

Substituting (3) into (4) then gives

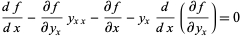(5)

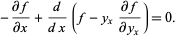(6)

This form is especially useful if 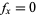, since in that case

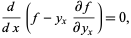(7)

which immediately gives

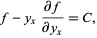(8)

where 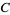 is a constant of integration (Weinstock 1974, pp. 24-25; Arfken 1985, pp. 928-929; Fox 1988, pp. 8-9).

The Beltrami identity greatly simplifies the solution for the minimal area surface of revolution about a given axis between two specified points. It also allows straightforward solution of the brachistochrone problem.

REFERENCES:

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, 1985.

Fox, C. An Introduction to the Calculus of Variations. New York: Dover, 1988.

Weinstock, R. Calculus of Variations, with Applications to Physics and Engineering. New York: Dover, 1974.